【题目】如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:
(1)旋转中心;
(2)旋转角度数;
(3)图中经过旋转后能重合的三角形共有几对?若A、O、C三点不共线,结论还成立吗?为什么?
(4)求当△BOC为等腰直角三角形时的旋转角度;
(5)若∠A=15°,则求当A、C、B在同一条线上时的旋转角度.

参考答案:
【答案】(1)旋转中心是点O;
(2旋转角度数是60°;
(3)△BOE与△COF不一定重合,结论不一定成立,理由见解析;
(4)旋转角度为:90°,
(5)旋转角度为120°.
【解析】试题分析:(1) △AOB与△COD是能够重合的图形,根据旋转的性质,即可求解,
(2)根据旋转的性质,得出旋转角的度数,
(3)根据旋转的性质得出能够重合的三角形,
(4)当△BOC为等腰三角形时,所以∠BOC=∠AOD=90°,根据旋转的性质,即可解答,
(5)根据旋转的性质即可解答.
试题解析:
(1)∵△AOB与△COD是能够重合的图形,
∴旋转中心是点O,
(2)根据题意得:旋转角是∠AOD或∠BOC,
∴旋转角度数是60°,
(3)经过旋转后能重合的三角形有△AOB与△DOC,△AOE与△DOF,△BOE与△COF共三对,
若A,O,C三点不共线,△AOE与△DOF,△BOE与△COF不一定重合,结论不一定成立,
∵若A,O,C三点不共线,∠DOB≠60°,
∴∠AOD=∠BOC=60°≠∠DOB,
∴△BOE与△COF不一定重合,结论不一定成立,
(4)∵△BOC为等腰直角三角形,
∴∠BOC=∠AOD=90°,
∴旋转角度为:90°,
(5)∵180°﹣∠BOC=180°﹣60°=120°,
∴旋转角度为120°.
-
科目: 来源: 题型:
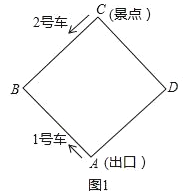
查看答案和解析>>【题目】如图,某景区内的环形路是边长为1200米的正方形ABCD,现有1号、2号两辆游览车分别从出口A和景点C同时出发,1号车沿A→B→C→D→A路线、2号车沿C→B→A→D→C路线连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为300米/分.
(1)如图1,设行驶时间为t分(0≤t≤8)
①1号车、2号车离出口A的路程分别为_____米,_____米;(用含t的代数式表示)
②当两车相距的路程是600米时,求t的值;
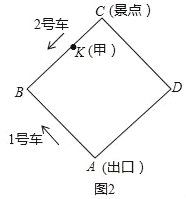
(2)如图2,游客甲在BC上的一点K(不与点B、C重合)处候车,准备乘车到出口A,设CK=x米.
情况一:若他刚好错过2号车,则他等候并搭乘即将到来的1号车;
情况二:若他刚好错过1号车,则他等候并搭乘即将到来的2号车.
请判断游客甲在哪种情况下乘车到出口A用时较多?(含候车时间)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )

A. ∠1=∠2+∠A B. ∠1=2∠A+∠2
C. ∠1=2∠2+2∠A D. 2∠1=∠2+∠A
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在大小为4×4的正方形网格中,是相似三角形的是( )

A. ①和② B. ②和③ C. ①和③ D. ②和④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD(___ ___)
∴∠2=∠CGD(等量代换)
∴CE∥BF(__ ___)
∴∠____ ____=∠BFD(___ ____)
又∵∠B=∠C(已知)
∴____ ____(等量代换)
∴AB∥CD(___ ____)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB∥CD,直线EF分别交AB,CD于点G,H,GM,HN分别为∠BGE和∠DHG的平分线.
(1)试判断GM和HN的位置关系;
(2)如果GM是∠AGH的平分线,(1)中的结论还成立吗?
(3)如果GM是∠BGH的平分线,(1)中的结论还成立吗?如果不成立,你能得到什么结论?

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正五边形与一个正方形的边长正好相等,在它们相接的地方,形成一个完整的“苹果”图案(如图).如果让正方形沿着正五边形的四周滚动,并且始终保持正方形和正五边形有两条边邻接,那么第一次恢复“苹果”的图形时,正方形要绕五边形转( )圈.
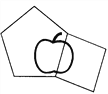
A. 4 B. 3 C. 6 D. 8
相关试题

