【题目】如图,在□ABCD中,点E,F是对角线BD上的两点,且BE=DF.
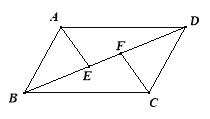
求证:(1)△ABE≌△CDF;(2)AE∥CF.
参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据平行四边形得出AB=CD,AB∥CD,即∠ABE=∠CDF,结合BE=DF可得△ABE≌△CDF;(2)、根据全等得出∠AEB=∠CFD,然后得出∠AED=∠CFB,从而说明答案.
试题解析:(1)、∵ 四边形ABCD是平行四边形
∴AB=CD,AB∥CD
∴∠ABE=∠CDF
∵BE=DF
∴△ABE≌△CDF(SAS)
(2)、∵△ABE≌△CDF(SAS)
∴∠AEB=∠CFD
∴180°-∠AEB=180°-∠CFD,
即∠AED=∠CFB
∴AE//CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年4月,生物学家发现一种病毒的长度约为0.0000043米,利用科学记数法表示为( )
A. 4.3×106米 B. 4.3×10﹣5米 C. 4.3×10﹣6米 D. 43×107米
-
科目: 来源: 题型:
查看答案和解析>>【题目】截止目前为止,世界人口约为73.5亿人,用科学记数法表示为7.35×10n人,则n=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题9分)为了了解“通话时长”(“通话时长”指每次通话时间)的分布情况,小强收集了他家1000个“通话时长”数据,这些数据均不超过18(单位:分钟),他从中随机抽取了若干个数据作为样本,统计结果如下表,并绘制了不完成的频数分布直方图.
“通话时长”
x/分钟
0<x≤3
3<x≤6
6<x≤9
9<x≤12
12<x≤15
15<x≤18
次数
36
a
8
12
8
12
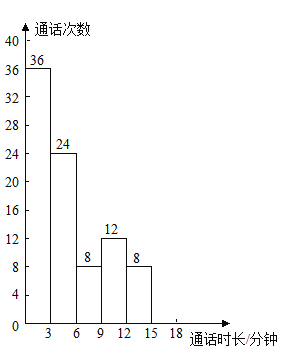
根据图、表提供的信息,解答下列问题:
(1)a= ,样本容量是 ,并将这个频数分布直方图补充完整;
 (2)求样本中“通话时长”不超过9分钟的频率;
(2)求样本中“通话时长”不超过9分钟的频率;(3)请估计小强家这1000次通话中“通话时长”超过15分钟的次数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠B=30°,CD,CE分别是AB边上的中线和高.

(1)求证:AE=ED;
(2)若AC=2,求△CDE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BC,且∠D=∠B;④AD∥BC,且∠BAD=∠BCD.其中,能推出AB∥DC的条件为( )

A.① B.② C.②③ D.②③④
相关试题

