【题目】如图,∠AOB是平角,射线OD平分∠AOC,射线OE平分∠BOD,且∠BOC=4∠AOD,求∠COE的度数. 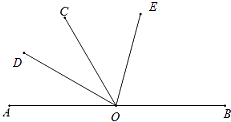
参考答案:
【答案】解:∵OD平分∠AOC,
∴∠AOD=∠COD= ![]() ∠AOC,
∠AOC,
∵∠BOC=4∠AOD,
∴∠BOC=2∠AOC,
∵∠BOC+∠AOC=180°,
∴3∠AOC=180°,
∴∠AOC=60°,
∴∠COD= ![]() ∠AOC=30°,∠BOC=2∠AOC=120°
∠AOC=30°,∠BOC=2∠AOC=120°
∴∠BOD=150°,
∵OE平分∠BOD,
∴∠EOD=∠BOE=75°,
∴∠COE=∠DOE﹣∠COD=75°﹣30°=45°
【解析】由OD平分∠AOC和∠BOC=4∠AOD,可求出∠AOC=60°,再求出∠COB的度数,即可求出∠BOD,利用∠COE=∠DOE﹣∠COD即可求出.
【考点精析】掌握角的平分线是解答本题的根本,需要知道从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2﹣2x+m﹣1=0有两个相等的实数根,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(﹣2,3)向右平移3个单位长度后的坐标为( )
A.(3,6)
B.(1,3)
C.(1,6)
D.(6,6) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方x程x2+ax+a﹣2=0.
(1)当该方程的一个根为1时,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C,D两点将线段AB分成2:3:4三部分,E为线段AB的中点,AD=10cm.求:
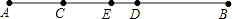
(1)线段AB的长;
(2)线段DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A
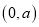 ,B
,B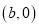 ,C
,C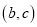 三点,其中a、b、c满足关系式
三点,其中a、b、c满足关系式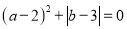 ,
, 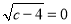 .
.(1) a= ;b= ;c= .
(2) 如果在第二象限内有一点P
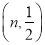 ,请用含
,请用含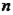 的式子表示四边形ABOP的面积;
的式子表示四边形ABOP的面积;(3) 在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=-2,a-b=4,则a2-b2=
相关试题

