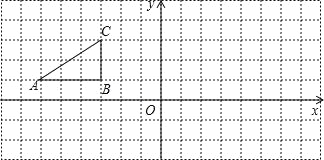
【题目】如图,方格纸中的每个小方格都是正方形,△ABC的顶点均在格点上,建立平面直角坐标系.
(1)以原点O为对称中心,画出与△ABC关于原点O对称的△A1B1C1,A1的坐标是 .
(2)将原来的△ABC绕着点(﹣2,1)顺时针旋转90°得到△A2B2C2,试在图上画出△A2B2C2的图形.
参考答案:
【答案】(1)(6,﹣1)(2)作图见解析
【解析】
试题分析:(1)连接AO并延长至A1,使A1O=AO,连接BO并延长至B1,使B1O=BO,连接CO并延长至C1,使C1O=CO,然后顺次连接A1、B1、C1即可得到△A1B1C1;再根据平面直角坐标系的特点写出点A1的坐标即可;
(2)根据旋转变换,找出点A、B、C绕点(﹣2,1)顺时针旋转90°后的对应点A2、B2、C2的位置,然后顺次连接即可.
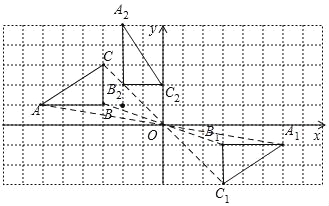
试题解析:(1)如图所示,△A1B1C1即为所求三角形,点A1的坐标是A1(6,﹣1);
故答案为:(6,﹣1);
(2)如图所示,△A2B2C2即为所求作的三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)(1)如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标_____(用含a的代数式表示);
(2)如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图2,求证:MD=MN.如何突破这种定势,获得问题的解决,请你写出你的证明过程.
(3)如图3,请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x,y互为相反数,m,n互为倒数,且有|a﹣2|=3,试求下面代数式的值:a2﹣(x+y+mn)a+(x+y)2017﹣(﹣mn)2017.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一组数据-1,0,2,4,x的极差为7,则x的值是( )
A. -3 B. 6 C. 7 D. 6或-3
-
科目: 来源: 题型:
查看答案和解析>>【题目】据统计,2017年上海市全社会用于环境保护的资金约为62800000000元,这个数用科学记数法表示为( )
A. 628×108 B. 62.8×109 C. 6.28×1010 D. 6.28×1011
-
科目: 来源: 题型:
查看答案和解析>>【题目】任意抛掷一枚骰子两次,骰子停止转动后,计算朝上的点数的和.
(1)和最小的是多少,和最大的是多少?
(2)下列事件:①点数的和为7;②点数的和为1;③点数的和为15.哪些是不可能性事件?哪些是不确定事件?
(3)点数的和为7与点数的和为2的可能性谁大?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
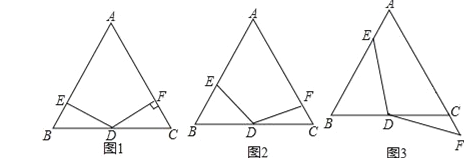
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF=
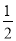 AB.
AB.(3)如图3,若∠EDF的两边分别交AB、AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE、AB、CF之间的数量关系.
相关试题

