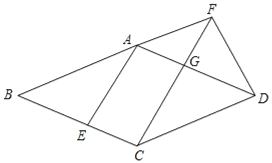
【题目】已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G.
求证:(1)FD=CG;
(2)CG2=FGFC.
参考答案:
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)先由菱形性质得∠FAD=∠B,再由全等三角形的判定定理得△ADF≌△BAE,进而得到FD=EA,由两组对边分别平行的四边形是平行四边形得到结论;(2)由两直线平行内错角相等得到∠DCF=∠BFC,由两直线平行同位角相等得到∠BAE=∠BFC,进而∠DCF=∠BAE,由全等三角形对应角相等得到∠BAE=∠FDA,∠DCF=∠FDA,再由相似三角形的判定得到△FDG∽△FCD,由相似性质得到结论.
试题解析:证明:(1)∵在菱形ABCD中,AD//BC,∴∠FAD=∠B,
又∵AF=BE,AD=BA,∴△ADF≌△BAE.
∴FD=EA,
∵CF//AE,AG//CE,∴EA=CG.
∴FD=CG.
(2)∵在菱形ABCD中,CD//AB,∴∠DCF=∠BFC.
∵CF//AE,∴∠BAE=∠BFC,∴∠DCF=∠BAE.
∵△ADF≌△BAE,∴∠BAE=∠FDA,∴∠DCF=∠FDA.
又∵∠DFG=∠CFD,∴△FDG∽△FCD.
∴![]() ,
, ![]() .
.
∵FD=CG, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,AE∥CD,CE∥AB,判断四边形ADCE的形状,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】中午,小明和小星两名同学结伴回家,路上,小星突然问:“你能判断空中的两根电线是否平行吗?”小明抬头看了看空中的电线:“呀,太高了!怎么判断呢?”小明苦思无法,聪明的你有什么解决的办法吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,DE是AC的中垂线,AE=3cm,△ABD的周长为13cm,则△ABC的周长是cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,面积为8cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中四边形ACED的面积是cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(1,3)关于原点O对称的点A′的坐标为( )
A.(-1,3)
B.(1,-3)
C.(3,1)
D.(-1,-3) -
科目: 来源: 题型:
查看答案和解析>>【题目】钟面上12点30分,时针与分针的夹角是( )
A. 150° B. 165° C. 170° D. 175°
相关试题

