【题目】如图,点A、B、C在半径为9的⊙O上, 弧AB的长为2π , 则∠ACB的大小是.
参考答案:
【答案】20°
【解析】解答: 连结OA、OB.设∠AOB=n°.
∵ 弧AB的长为2π ,
∴ ![]() n×π×9
n×π×9
∴n=40,
∴∠AOB=40°,
∴∠ACB= ![]() ∠AOB=20°.
∠AOB=20°.
所以答案是20°.
连结OA、OB.先由弧AB的长为2π,利用弧长计算公式求出∠AOB=40°,再根据在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半得到∠ACB= ![]() ∠AOB=20°.
∠AOB=20°.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半),还要掌握弧长计算公式(若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知O为直线AB上一点,OC平分∠AOD,∠BOD=3∠DOE,∠COE=α,则∠BOE的度数为( )

A. α B. 180°﹣2α C. 360°﹣4α D. 2α﹣60°
-
科目: 来源: 题型:
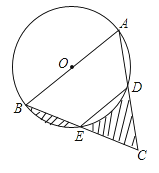
查看答案和解析>>【题目】如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( ).
A.
B.2
C.
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】将6张小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.当AB长度不变而BC变长时,将6张小长方形纸片还按照同样的方式放在新的长方形ABCD内,S1与S2的差总保持不变,则a,b满足的关系是

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上.若∠BAD=120°,则弧BC的长度等于 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】边长为4cm的正方形ABCD绕它的顶点A旋转180°,顶点B所经过的路线长为 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了表示对老师的敬意,张昊同学特地做了两张大小不同的正方形的画送给老师,其中一张面积为800 cm2,另一张面积为450 cm2.他想:如果再用金色细彩带把画的边镶上会更漂亮.他手上现有1.2 m长的金色细彩带.请你帮他算一算,他的金色细彩带够用吗?如果不够用,还需买多少厘米的金色细彩带?(
 ≈1.414,结果保留整数)
≈1.414,结果保留整数)
相关试题

