【题目】在平面直角坐标系中,已知两个点A(3,0),B(0,2)所在直线为L,请写出在y轴上使△ABP为等腰三角形的P点坐标 .
参考答案:
【答案】(0,﹣ ![]() )、(0,2+
)、(0,2+ ![]() )、(0,﹣2)
)、(0,﹣2)
【解析】解:∵A(3,0),B(0,2), ∴AB= ![]() =
= ![]() ,
,
①以AB为底时,
作出线段AB的垂直平分线和y轴交于P点,
∴点P的坐标为(0,﹣ ![]() ).
).
②以AB为腰时,符合条件的点P的坐标是:(0,2+ ![]() ),(0,﹣2),
),(0,﹣2),
综上所述,满足条件的P的坐标是:(0,﹣ ![]() )、(0,2+
)、(0,2+ ![]() )、(0,﹣2).
)、(0,﹣2).
所以答案是:(0,﹣ ![]() )、(0,2+
)、(0,2+ ![]() )、(0,﹣2).
)、(0,﹣2).
【考点精析】根据题目的已知条件,利用等腰三角形的判定的相关知识可以得到问题的答案,需要掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的底面半径为3cm,母线长为5cm,则圆锥的侧面积是( )
A.20cm2
B.20πcm2
C.15cm2
D.15πcm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为反比例函数y=
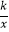 的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图像上的是( )
的图像上一点,PA⊥x轴于点A,△PAO的面积为6,则下列各点中也在这个反比例函数图像上的是( ) 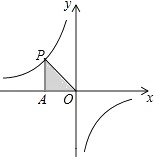
A.(2,3)
B.(﹣2,6)
C.( 2,6 )
D.(﹣2,3) -
科目: 来源: 题型:
查看答案和解析>>【题目】某地电话拨号入网有两种收费方式,用户可以任选其一:
(A)计时制:0.05元/分;
(B)包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为
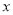 分,请你用含
分,请你用含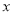 的代数式分别写出两种收费方式下该用户应该支付的费用;
的代数式分别写出两种收费方式下该用户应该支付的费用;(2)如果某用户一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】⑴例:代数式
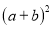 表示
表示 、
、 两数和的平方. 仿照上例填空:
两数和的平方. 仿照上例填空:代数式
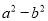 表示________________________________________.
表示________________________________________.代数式
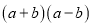 表示________________________________________.
表示________________________________________.⑵试计算
 、
、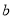 取不同数值时,
取不同数值时, 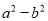 及
及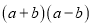 的植, 填入下表:
的植, 填入下表: 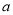 、
、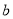 的值
的值当
 =3,
=3, 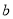 =2时
=2时当
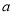 =-5,
=-5, 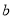 =1时
=1时当
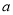 =-2,
=-2, 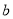 =-5时
=-5时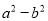
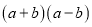
⑶请你再任意给
 、
、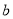 各取一个数值, 并计算
各取一个数值, 并计算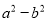 及
及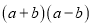 的植:
的植: 当
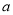 =_____,
=_____,  =______时,
=______时, 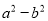 =_________,
=_________, 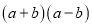 =__________.
=__________.⑷我的发现: ______________________________.
⑸用你发现的规律计算:
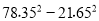
-
科目: 来源: 题型:
查看答案和解析>>【题目】用计算机处理数据,为了防止数据输入出错,某研究室安排两位程序操作员各输入一遍,比较两人的输入是否一致,两人各输入2640个数据,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完,这两个操作员每分钟各能输入多少个数据?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点,△A′BO′、△A′BP′分别由△AOB、△APB旋转而得,旋转角都为60°,则下列结论中正确的有( ).(提示:有一个角是60°的等腰三角形是等边三角形)
①△O′BO为等边三角形,且A′、O′、O、C在一条直线上.
②A′O′+O′O=AO+BO. ③A′P′+P′P=PA+PB.
④PA+PB+PC>AO+BO+CO.
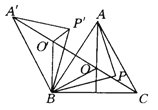
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

