【题目】如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.

参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、由AD⊥BC,CE⊥AB,易得∠AFE=∠B,利用全等三角形的判定得△AEF≌△CEB;
(2)、由全等三角形的性质得AF=BC,由等腰三角形的性质“三线合一”得BC=2CD,等量代换得出结论.
试题解析:(1)、∵AD⊥BC,CE⊥AB, ∴∠BCE+∠CFD=90°,∠BCE+∠B=90°, ∴∠CFD=∠B,
∵∠CFD=∠AFE, ∴∠AFE=∠B 在△AEF与△CEB中,  ,
,
∴△AEF≌△CEB(AAS);
(2)、∵AB=AC,AD⊥BC, ∴BC=2CD, ∵△AEF≌△CEB, ∴AF=BC, ∴AF=2CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为_________每千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面正确的命题中,其逆命题不成立的是 ( )
A.同旁内角互补,两直线平行
B.全等三角形的对应边相等
C.角平分线上的点到这个角的两边的距离相等
D.对顶角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题:①两直线平行,内错角相等;②对顶角相等;③等腰三角形的两个底角相等;④菱形的对角线互相垂直,其中逆命题是真命题的是( )
A. ①②③④B. ①③④C. ①③D. ①
-
科目: 来源: 题型:
查看答案和解析>>【题目】 定义:两组邻边分别相等的四边形叫做筝形.
(1)、请写出除定义外的性质和判定猜想各一条,并从定义出发证明你的判定猜想.
(2)、筝型ABCD中,对角线AC,BD相交于点O.
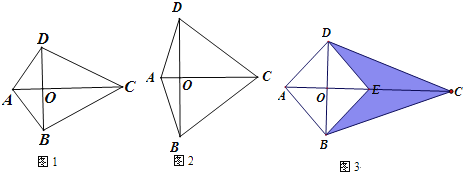
①如图1,若BD=CO,求tan∠BCD的值.
②如图2,若∠DAC=∠BCD=72,求AD:CD的值.
(3)、如图3,把△ABD沿着对角线BD翻折,A点落在对角线AC上的E点.如果△AOD中,一个内角是另一个内角的2倍,且阴影部分图形的面积等于四边形ABED的面积,直接写出
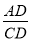 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=3(x-2)2的开口方向是______,顶点坐标为______,对称轴是______.当x______时,y随x的增大而增大;当x=______时,y有最______值是______,它可以由抛物线y=3x2向______平移______个单位得到.
-
科目: 来源: 题型:
查看答案和解析>>【题目】16的算术平方根是_______.
相关试题

