【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,连接BE、DF,DF交对角线AC于点G,且DE=DG.
(1)求证:AE=CG;
(2)试判断BE和DF的位置关系,并说明理由.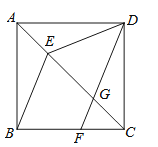
参考答案:
【答案】解:(1)证明:在正方形ABCD中,
∵AD=CD,
∴∠DAE=∠DCG,
∵DE=DG,
∴∠DEG=∠DGE,
∴∠AED=∠CGD.
在△AED和△CGD中,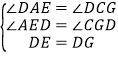
∴△AED≌△CGD(AAS),
∴AE=CG.
(2)解法一:BE∥DF,理由如下:
在正方形ABCD中,AB∥CD,
∴∠BAE=∠DCG.
在△AEB和△CGD中,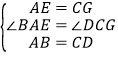
∴△AEB≌△CGD(SAS),
∴∠AEB=∠CGD.
∵∠CGD=∠EGF,
∴∠AEB=∠EGF,
∴BE∥DF.
解法二:BE∥DF,理由如下:
在正方形ABCD中,
∵AD∥FC,
∴![]() =
=![]() .
.
∵CG=AE,
∴AG=CE.
又∵在正方形ABCD中,AD=CB,
∴![]() =
=![]() .
.
又∵∠GCF=∠ECB,
∴△CGF∽△CEB,
∴∠CGF=∠CEB,
∴BE∥DF.
【解析】(1)先证∠AED=∠CGD,再证明△ADE≌△CDG,根据全等三角形的对应边相等即可得出结论;
(2)先证明△AEB≌△CGD,得出对应角相等∠AEB=∠CGD,得出∠AEB=∠EGF,即可证出平行线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,直线a∥b∥c∥d,且a与b,c与d之间的距离均为1,b与c之间的距离为2,现将正方形ABCD如图放置,使其四个顶点分别在四条直线上,求正方形的边长;
(2)在(1)的条件下,探究:将正方形ABCD改为菱形ABCD,如图2,当∠DCB=120°时,求菱形的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据4、4、4、5、5、6、7的众数和中位数分别是( )
A.4和4B.4和5C.7和5D.7和6
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是900°,这个多边形的边数是( )
A.10
B.9
C.8
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形ABCD中,对角线AC与BD相交于点O,∠BAD=120°,AC=4,则该菱形的面积是( )
A.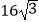
B.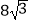
C.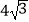
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算4y·(-2xy2)的结果等于__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较大小:-3______-0.1.
相关试题

