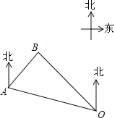
【题目】如图,一艘巡逻船在海上![]() 处巡航,突然接到海上指挥中心
处巡航,突然接到海上指挥中心![]() 处发出的紧急通知,在巡逻船的东北方向的
处发出的紧急通知,在巡逻船的东北方向的![]() 处有一艘渔船遇险,要马上前去救援,已知点
处有一艘渔船遇险,要马上前去救援,已知点![]() 位于指挥中心
位于指挥中心![]() 的北偏西
的北偏西![]() 方向上,且相距
方向上,且相距![]() 海里,渔船位于指挥中心
海里,渔船位于指挥中心![]() 的北偏西
的北偏西![]() 方向上,求
方向上,求![]() 、
、![]() 两地之间的距离.(结果精确到
两地之间的距离.(结果精确到![]() 海里,参考数据:
海里,参考数据:![]() ,
,![]() ,
,![]() )
)
参考答案:
【答案】![]() 、
、![]() 两地之间的距离约为
两地之间的距离约为![]() 海里
海里
【解析】
作BC⊥OA于点C,根据题意得∠MAB=45°,∠NOA=60°,∠NOB=30°,OA=60海里.由AM∥ON,求出∠BAO=∠MAO-∠MAB=75°,根据三角形内角和定理得出∠ABO=180°-∠BAO-∠AOB=75°,利用等角对等边得到OB=OA=60海里,在直角△OBC中根据含30°角的直角三角形的性质得出BC=![]() OB=30海里,OC=
OB=30海里,OC=![]() BC=30
BC=30![]() 海里,那么AC=OA-OC=(60-30
海里,那么AC=OA-OC=(60-30![]() )≈8.04海里,然后根据勾股定理求出AB=
)≈8.04海里,然后根据勾股定理求出AB=![]() ≈31.1海里.
≈31.1海里.
如图,作BC⊥OA于点C,
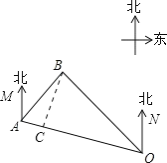
根据题意得∠MAB=45,∠NOA=60,∠NOB=30,OA=60海里,
∵AM∥ON,
∴∠MAO+∠NOA=180,
∴∠MAO=180∠NOA=120,
∴∠BAO=∠MAO∠MAB=75,
∵∠AOB=∠NOA∠NOB=30,
∴∠ABO=180∠BAO∠AOB=75,
∴∠BAO=∠ABO=75,
∴OB=OA=60海里,
∴BC=![]() OB=30海里,OC=
OB=30海里,OC=![]() BC=30
BC=30![]() 海里,
海里,
∴AC=OAOC=(6030![]() )≈8.04海里,
)≈8.04海里,
∴AB=![]() ≈
≈![]() ≈31.1海里.
≈31.1海里.
答:A、B两地之间的距离约为31.1海里.
-
科目: 来源: 题型:
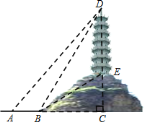
查看答案和解析>>【题目】如图,小明为了测量小山顶的塔高,他在
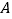 处测得塔尖
处测得塔尖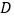 的仰角为
的仰角为 ,再沿
,再沿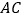 方向前进
方向前进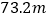 到达山脚
到达山脚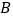 处,测得塔尖
处,测得塔尖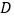 的仰角为
的仰角为 ,山坡
,山坡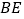 的坡度
的坡度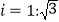 ,求塔高.(精确到
,求塔高.(精确到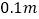 ,
,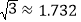 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】水务部门为加强防汛工作,决定对某水库大坝进行加固.原大坝的横截面是梯形ABCD,如图所示,已知迎水面AB的长为10米,∠B=60°,背水面DC的长度为
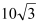 米,加固后大坝的横截面是梯形ABED,CE的长为5米.
米,加固后大坝的横截面是梯形ABED,CE的长为5米.
(1)已知需加固的大坝长为100米,求需要填方多少立方米;
(2)求新大坝背水面
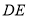 的坡度.(计算结果保留根号)。
的坡度.(计算结果保留根号)。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=8,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=a,DE交AC于点E,下列结论:①AD2=AE.AB;②1.8≤AE<5;⑤当AD=
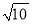 时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
时,△ABD≌△DCE;④△DCE为直角三角形,BD为4或6.25.其中正确的结论是_____.(把你认为正确结论序号都填上)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1、x2,其中﹣2<x1<﹣1,0<x2<1.下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③abc<0;④b2+8a<4ac.
其中正确的结论有( )
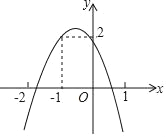
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实党中央“长江大保护”新发展理念,我市持续推进长江岸线保护,还洞庭湖和长江水清岸绿的自然生态原貌.某工程队负责对一面积为33000平方米的非法砂石码头进行拆除,回填土方和复绿施工,为了缩短工期,该工程队增加了人力和设备,实际工作效率比原计划每天提高了20%,结果提前11天完成任务,求实际平均每天施工多少平方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有_____名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为_____;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.

相关试题

