【题目】如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到1000个小三角形,则需要操作的次数是( ) 
A.332
B.333
C.334
D.335
参考答案:
【答案】B
【解析】解:∵第一次操作后,三角形共有4个; 第二次操作后,三角形共有4+3=7个;
第三次操作后,三角形共有4+3+3=10个;
…
∴第n次操作后,三角形共有4+3(n﹣1)=3n+1个;
当3n+1=1000时,解得:n=333,
故选:B.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的进价为800元,出售是标价为1200元,后来由于该商品积压,商品准备打折销售,但是保证利润率不低于5%,则至少可打( )
A.6折B.7折C.8折D.9折
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(﹣3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.

(1)求点C的坐标和直线l1的解析式;
(2)若将点C先向左平移3个单位长度,再向上平移6个单位长度得到点D,请你判断点D是否在直线l1上;
(3)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90,当点D在线段BC上时(与点B不重合),如图2,线段CF,BD所在直线位置关系为 ,数量关系为 .
(2)如果AB=AC,∠BAC=90,当点D在线段BC的延长线时,如图3,(1)中的结论是否仍然成立,并说明理由。
(3)如果AB=AC,∠BAC是钝角,点D在线段BC上,当∠ABC满足什么条件时,CF⊥BC(点C、F不重合)画出图形,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )

A. y=x+12 B. y=0.5x+12
C. y=0.5x+10 D. y=x+10.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣1,﹣2),点B(1,4)
(1)试建立相应的平面直角坐标系;
(2)描出线段AB的中点C,并写出其坐标;
(3)将线段AB沿水平方向向右平移3个单位长度得到线段A1B1,写出线段A1B1两个端点及线段中点C1的坐标.
-
科目: 来源: 题型:
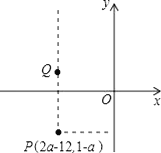
查看答案和解析>>【题目】已知点P(2a﹣12,1﹣a)位于第三象限,点Q(x,y)位于第二象限且是由点P向上平移一定单位长度得到的.
(1)若点P的纵坐标为﹣3,试求出a的值;
(2)在(1)题的条件下,试求出符合条件的一个点Q的坐标;
(3)若点P的横、纵坐标都是整数,试求出a的值以及线段PQ长度的取值范围.
相关试题

