【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①a,b同号;②当x=1和x=3时,函数值相等;③4a+b=0;④当y=﹣2时,x的值只能取2;
⑤当﹣1<x<5时,y<0.其中正确的有( )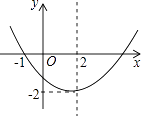
A.2个
B.3个
C.4个
D.5个
参考答案:
【答案】C
【解析】解:①∵抛物线的开口方向向上,
∴a>0,
∵对称轴为x= ![]() =2>0,
=2>0,
又∵a>0,
∴b<0,
即a,b异号,错误;
②∵x=1和x=3关于x=2对称,
∴当x=1和x=3时,函数值相等,正确;
③∵x= ![]() =2,
=2,
∴b=﹣4a,
即4a+b=0,正确;
④∵y=﹣2正好为抛物线顶点坐标的纵坐标,
∴当y=﹣2时,x的值只能取2,正确;
⑤∵对称轴为x=2,
∴x=﹣1和x=5关于x=2对称,
故当﹣1<x<5时,y<0.
∴②、③、④、⑤正确.
故选C.
【考点精析】根据题目的已知条件,利用二次函数的图象的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=150°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图1.第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图2.照此下去,至多能进行( )步.
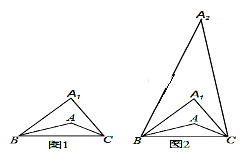
A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在双曲线y=
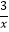 上,点B在双曲线y=
上,点B在双曲线y= 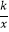 (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
A.6
B.9
C.10
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明要测量河内小岛B到河边公路AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,求小岛B到公路AD的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,身高1.6米的小明从距路灯的底部(点O)20米的点A沿AO方向行走14米到点C处,小明在A处,头顶B在路灯投影下形成的影子在M处.
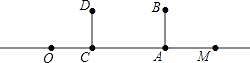
(1)已知灯杆垂直于路面,试标出路灯P的位置和小明在C处,头顶D在路灯投影下形成的影子N的位置.
(2)若路灯(点P)距地面8米,小明从A到C时,身影的长度是变长了还是变短了?变长或变短了多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,﹣2),反比例函数y=
 的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
(1)求反比例函数与一次函数的解析式;
(2)求反比例函数与一次函数的另一个交点M的坐标;
(3)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
相关试题

