【题目】【课本引申】
我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
【尝试探究】
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?

【拓展运用】
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,若∠1+∠2=230°,则剪掉的∠C=_________;

(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请直接写出答案_ .

(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)

参考答案:
【答案】(1)∠DBC+∠ECB =180°+∠A (2)50°(3)∠P=90°-![]() ∠A (4)∠BAD+∠CDA=360°-2∠P.
∠A (4)∠BAD+∠CDA=360°-2∠P.
【解析】试题分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;
(2)根据(1)的结论整理计算即可得解;
(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;
(4)延长BA、CD相交于点Q,先用∠Q表示出∠P,再用(1)的结论整理即可得解;
试题解析:
(1)∠DBC+∠ECB=180°-∠ABC+180°-∠ACB
=360°-(∠ABC+∠ACB)
=360°-(180°-∠A)
=180°+∠A
(2)50°
(3)∠P=90°-![]() ∠A
∠A
(4)延长BA、CD交于点Q,
则∠P=90°-![]() ∠Q,∴∠Q=180°-2∠P.
∠Q,∴∠Q=180°-2∠P.
∴∠BAD+∠CDA=180°+∠Q=180°+180°-2∠P=360°-2∠P.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于三个数a,b,c,M
 表示a,b,c这三个数的平均数,min
表示a,b,c这三个数的平均数,min 表示a,b,c这三个数中最小的数,如:
表示a,b,c这三个数中最小的数,如: M
 ,min
,min =-1;
=-1;M
 ,min
,min =
= ;
;解决下列问题:
(1) 填空:min{ a, a-1, a+2 }=______________;
(2) 若min
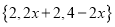 =2,则x的取值范围是______________;
=2,则x的取值范围是______________;(3) ①若M
 =min
=min ,那么x=______________;
,那么x=______________;②根据①,你发现结论“若M
 =min
=min ,则______________;(填a,b,c的大小关系);
,则______________;(填a,b,c的大小关系);③运用②解决问题:(写出求解的过程)
若M
 =min
=min ,
,求x+y 的值.
-
科目: 来源: 题型:
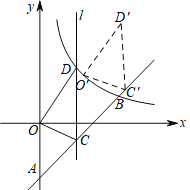
查看答案和解析>>【题目】如图,一次函数y=kx-4(k≠0)的图象与y轴交于点A,与反比例函数y=
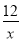 (x>0)的图象交于点B(6,b).
(x>0)的图象交于点B(6,b).(1)b=__________;k=__________.
(2)点C是直线AB上的动点(与点A,B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,当点C的横坐标为3时,得△OCD,现将△OCD沿射线AB方向平移一定的距离(如图),得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上,求点O′,D′的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=
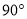 ,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.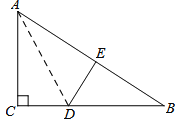
(1)问:△BDE与△BAC相似吗?
(2)已知AC=6,BC=8,求线段AD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某小区内有一块长、宽比为2∶1的矩形空地,计划在该空地上修筑两条宽均为2 m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312 m2,请求出原来大矩形空地的长和宽.
(1)请找出上述问题中的等量关系:_________________;
(2)若设大矩形空地的宽为xm,可列出的方程为_____________,方程的解为__________,原来大矩形空地的长和宽分别为_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把
 平移至
平移至 的位置,使点
的位置,使点 与
与 对应,得到
对应,得到 ;
;(2)图中可用字母表示,与线段
 平行且相等的线段有哪些?
平行且相等的线段有哪些?(3)求四边形
 的面积.
的面积.
相关试题

