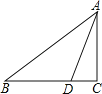
【题目】如图,Rt△ABC中,∠C=90°,BD=4,CD=2,∠ADB=3∠ABD,则AD= .
参考答案:
【答案】![]() .
.
【解析】
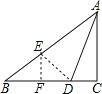
试题分析:如图,作BD的垂直平分线,交AB于点E,连接DE,设∠ABD=α,证明∠AED=∠ADE=2α,AE=AD;证明AE=2BE(设为2λ),得到AD=AE=2λ;利用勾股定理,可证明4λ2﹣4=9λ2﹣36,解得:λ=![]() ,求出AD即可解决问题.
,求出AD即可解决问题.
解:如图,作BD的垂直平分线,交AB于点E,连接DE,设∠ABD=α,设BE=λ,
则BE=DE=λ,BF=DF=2,CF=4;
∴∠ABD=∠EDB=α;
∵∠AED=∠ABD+∠EDB=2α,∠ADB=3∠ABD=3α,
∴∠AED=∠ADE=2α,AE=AD;
∵EF⊥BC,AC⊥BC,
∴EF∥AC,![]() =
=![]() =2,
=2,
∴AE=2BE=2λ,
∴AD=AE=2λ;
由勾股定理得:
AC2=AD2﹣DC2=4λ2﹣4,
AC2=AB2﹣BC2=9λ2﹣36,
∴4λ2﹣4=9λ2﹣36,
解得:λ=![]() ,
,
∴AD=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
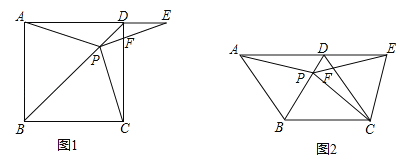
查看答案和解析>>【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.(1)求证:PC=PE; (2)求∠CPE的度数;
拓展探究
(3)如图2,把“正方形ABCD”改为“菱形ABCD”,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形是全等三角形的是( )
A.两个含60°角的直角三角形
B.腰对应相等的两个等腰直角三角形
C.边长为3和4的两个等腰三角形
D.一个钝角相等的两个等腰三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】64的立方根是( )
A. 8 B. 4 C. ﹣8 D. ±8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF∥CE.
(1)说明四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.

-
科目: 来源: 题型:
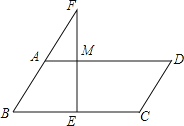
查看答案和解析>>【题目】如图,在ABCD中,边BC的垂直平分线EF分别交AD、BC于点M、E,交BA的延长线于点F,若点A是BF的中点,AB=5,ABCD的周长为34,则FM的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数y=x2的性质表达正确的一项是( )
A.无论x为任何实数,y值总为正
B.当x值增大时,y的值也增大
C.它的图象关于y轴对称
D.它的图象在第一、三象限内
相关试题

