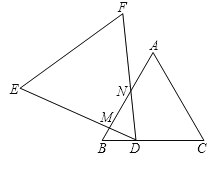
【题目】在正方形ABCD中,连接BD.
(1)如图1,AE⊥BD于E.直接写出∠BAE的度数.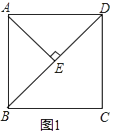
(2)如图1,在(1)的条件下,将△AEB以A旋转中心,沿逆时针方向旋转30°后得到△AB′E′,AB′与BD交于M,AE′的延长线与BD交于N.
①依题意补全图1;
②用等式表示线段BM、DN和MN之间的数量关系,并证明.
(3)如图2,E、F是边BC、CD上的点,△CEF周长是正方形ABCD周长的一半,AE、AF分别与BD交于M、N,写出判断线段BM、DN、MN之间数量关系的思路.(不必写出完整推理过程)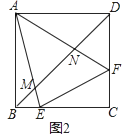
参考答案:
【答案】
(1)解:∵BD是正方形ABCD的对角线,
∴∠ABD=∠ADB=45°,
∵AE⊥BD,
∴∠ABE=∠BAE=45°,
(2)解:①依题意补全图形,如图1所示,
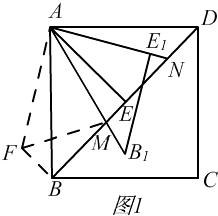
②BM、DN和MN之间的数量关系是BM2+MD2=MN2,
将△AND绕点D顺时针旋转90°,得到△AFB,
∴∠ADB=∠FBA,∠BAF=∠DAN,DN=BF,AF=AN,
∵在正方形ABCD中,AE⊥BD,
∴∠ADB=∠ABD=45°,
∴∠FBM=∠FBA+∠ABD=∠ADB+∠ABD=90°,
在Rt△BFM中,根据勾股定理得,FB2+BM2=FM2,
∵旋转△ANE得到AB1E1,
∴∠E1AB1=45°,
∴∠BAB1+∠DAN=90°﹣45°=45°,
∵∠BAF=DAN,
∴∠BAB1+∠BAF=45°,
∴∠FAM=45°,
∴∠FAM=∠E1AB1,
∵AM=AM,AF=AN,
∴△AFM≌△ANM,
∴FM=MN,
∵FB2+BM2=FM2,
∴DN2+BM2=MN2,
(3)解:如图2,
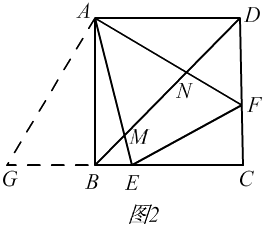
将△ADF绕点A顺时针旋转90°得到△ABG,
∴DF=GB,
∵正方形ABCD的周长为4AB,
△CEF周长为EF+EC+CF,
∵△CEF周长是正方形ABCD周长的一半,
∴4AB=2(EF+EC+CF),
∴2AB=EF+EC+CF
∵EC=AB﹣BE,CF=AB﹣DF,
∴2AB=EF+AB﹣BE+AB﹣DF,
∴EF=DF+BE,
∵DF=GB,
∴EF=GB+BE=GE,
由旋转得到AD=AG=AB,
∵AM=AM,
∴△AEG≌△AEF,
∠EAG=∠EAF=45°,
和(2)的②一样,得到DN2+BM2=MN2.
【解析】(1)利用正方形性质和等腰直角三角形性质可求出;(2)通过旋转构造全等三角形,即△AND全等于△AFB, 进而∠FBM=∠FBA+∠ABD=∠ADB+∠ABD=90°,得到△AFM≌△ANM,转化FM=MN,进而得出三边之间的勾股关系; (3)借鉴(2)的思路方法,仍可采用旋转法,构造全等三角形△ADF△ABG,进一步△AEG≌△AEF,得出三边之间的关系.
【考点精析】关于本题考查的勾股定理的概念,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两个等边△ABC和△DEF(DE>AB)如图所示摆放,点D是BC上的一点(除B、C点外).把△DEF绕顶点D顺时针旋转一定的角度,使得边DE、DF与△ABC的边(除BC边外)分别相交于点M、N.
(1)∠BMD和∠CDN相等吗?
(2)画出使∠BMD和∠CDN相等的所有情况的图形.
(3)在(2)题中任选一种图形说明∠BMD和∠CDN相等的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】收集和整理数据.
某中学七(1)班学习了统计知识后,数学老师要求每个学生就本班学生的上学方式进行一次全面调查,如图是一同学通过收集数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题:(每个学生只选择1种上学方式).

(1)求该班乘车上学的人数;
(2)将频数分布直方图补充完整;
(3)若该校七年级有1200名学生,能否由此估计出该校七年级学生骑自行车上学的人数,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5)B. (5,2)C. (2,﹣5)D. (5,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
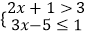 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A.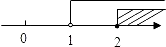
B.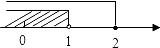
C.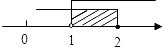
D.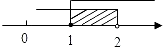
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b)(m≠1的实数).
其中正确的结论有( )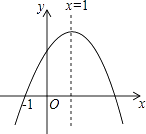
A.2个
B.3个
C.4个
D.5个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小满的一次作业,老师说小满的解题过程不完全正确,并在作业旁写出了批改.
长跑比赛中,张华跑在前面,在离终点
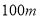 时他以
时他以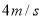 的速度向终点冲刺,在他身后
的速度向终点冲刺,在他身后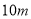 的李明需以多快的速度同时开始冲刺,才能在张华之前到达终点?
的李明需以多快的速度同时开始冲刺,才能在张华之前到达终点?解:设李明以
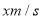 的速度开始冲刺,
的速度开始冲刺,依题意,得
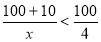 ,
,
两边同时除以25,得
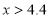 .
.答:李明需以大于
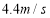 的速度同时开始冲刺,才能在张华之前到达终点.
的速度同时开始冲刺,才能在张华之前到达终点.请回答:必须添加“根据实际意义可知,
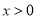 ”这个条件的理由是_______________________.
”这个条件的理由是_______________________.
相关试题

