【题目】如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点. 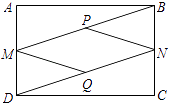
(1)求证:△MBA≌△NDC;
(2)求证:四边形MPNQ是菱形.
参考答案:
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠C=90°,
∵在矩形ABCD中,M、N分别是AD、BC的中点,
∴AM= ![]() AD,CN=
AD,CN= ![]() BC,
BC,
∴AM=CN,
在△MAB和△NDC中,
∵ 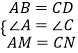 ,
,
∴△MBA≌△NDC(SAS)
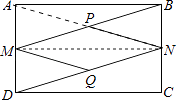
(2)证明:四边形MPNQ是菱形.
理由如下:连接AP,MN,
则四边形ABNM是矩形,
∵AN和BM互相平分,
则A,P,N在同一条直线上,
易证:△ABN≌△BAM,
∴AN=BM,
∵△MAB≌△NDC,
∴BM=DN,
∵P、Q分别是BM、DN的中点,
∴PM=NQ,
∵ 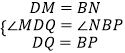 ,
,
∴△MQD≌△NPB(SAS).
∴四边形MPNQ是平行四边形,
∵M是AD中点,Q是DN中点,
∴MQ= ![]() AN,
AN,
∴MQ= ![]() BM,
BM,
∵MP= ![]() BM,
BM,
∴MP=MQ,
∴平行四边形MQNP是菱形.
【解析】(1)根据矩形的性质和中点的定义,利用SAS判定△MBA≌△NDC;(2)四边形MPNQ是菱形,连接AN,有(1)可得到BM=DN,再有中点得到PM=NQ,再通过证明△MQD≌△NPB得到MQ=PN,从而证明四边形MPNQ是平行四边形,利用三角形中位线的性质可得:MP=MQ,进而证明四边形MQNP是菱形
【考点精析】认真审题,首先需要了解菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形),还要掌握矩形的性质(矩形的四个角都是直角,矩形的对角线相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x的2倍与5的差不小于3,用不等式表示这一关系为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC是等腰直角三角形,∠ACB=90°,直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
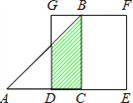
A.
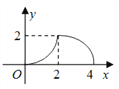 B.
B. 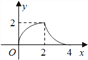 C.
C. 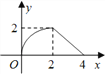 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学课上,老师要求学生根据图示张鑫与李亮的对话内容,展开如下活动:
活动1:仔细阅读对话内容
活动2:根据对话内容,提出一些数学问题,并解答.
下面是学生提出的两个问题,请你列方程解答.
(1)如果张鑫没有办卡,她需要付多少钱?
(2)你认为买多少元钱的书办卡就便宜? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
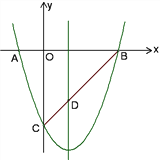
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ
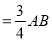 时,求tan∠CED的值;
时,求tan∠CED的值;②当以C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
(参考公式:抛物线
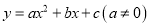 的顶点坐标是
的顶点坐标是 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一个数的相反数是它本身,则这个数是()
A. 0 B. 正数 C. 负数 D. 非负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有48位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数分布直方图(横半轴表示分数,把50.5分到100.5分之间的分数分成5组,组距是10分,纵半轴表示频数)如图所示,从左到右的小矩形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )
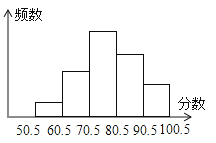
A.9
B.18
C.12
D.6
相关试题

