【题目】用边长为12cm的正方形硬纸板做三棱柱盒子,每个盒子的侧面为长方形,底面为等边三角形.
(1)每个盒子需 个长方形, 个等边三角形;
(2)硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.
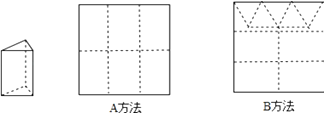
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
① 用x的代数式分别表示裁剪出的侧面和底面的个数;
② 若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
参考答案:
【答案】(1)3, 2;(2)①侧面的个数为(2x+76)个,底面的个数为(95-5x)个;②裁剪出的侧面和底面恰好全部用完,能做30个盒子.
【解析】试题分析:(1)由图可知每个三棱柱盒子需3个长方形,2个等边三角形;
(2)①由x张用A方法,就有(19-x)张用B方法,就可以分别表示出侧面个数和底面个数;
②由侧面个数和底面个数比为3:2,建立方程求出x的值,求出侧面的总数就可以求出结论.
试题解析:(1)观察可知每个盒子需要3个长方形,2个等边三角形,
故答案为:3, 2;
(2)①∵裁剪时x张用A方法,
∴裁剪时(19-x)张用B方法.
∴侧面的个数为:6x+4(19-x)=(2x+76)个,
底面的个数为:5(19-x)=(95-5x)个;
②由题意,得![]() ,
,
解得:x=7,
∴盒子的个数为: ![]() =30,
=30,
答:裁剪出的侧面和底面恰好全部用完,能做30个盒子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个顶点分别为A(-2,3),B(-4,-1),C(2,0),现将△ABC平移至△A′B′C′处,且点A′的坐标为(0,2),则点C′的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个相似三角形的面积之比是1:4,那么这两个三角形的周长之比是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
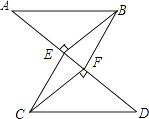
求证:
(1)BE=CF;
(2)四边形BECF是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程ax+3=1的解为x=2,则a的值为( )
A.1
B.﹣1
C.2
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣8x+10的图象的顶点坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算x2x3的结果是( )
A.x5
B.x8
C.x6
D.x7
相关试题

