【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.

参考答案:
【答案】DE=BF,DE⊥BF.理由见解析.
【解析】试题分析:本题首先要给出答案,在说明理由. 连接DB,根据DH是AB的垂直平分线得出∠A=∠DBH,再根据三角形外角的性质得出∠CDB=∠A+∠DBH,故可得出CD=CB.由SAS定理得出△ECD≌△FCB,所以ED=FB,∠DEC=∠BFC,∠DEC+∠FBC=90°,进而可得出结论.
试题解析:
DE=BF,DE⊥BF.
理由如下:
连接BD,延长BF交DE于点G.
∵点D在线段AB的垂直平分线上,∴AD=BD,
∴∠ABD=∠A=22.5°.
在Rt△ABC中,∵∠ACB=90°,∠A=22.5°,
∴∠ABC=67.5°,
∴∠CBD=∠ABC-∠ABD=45°,
∴△BCD为等腰直角三角形,
∴BC=DC.
又∵CE=CF,∴Rt△ECD≌Rt△FCB(SAS),
∴DE=BF,∠CED=∠CFB.
∵∠CFB+∠CBF=90°,∴∠CED+∠CBF=90°,
∴∠EGB=90°,即DE⊥BF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知△ABC.
(1)请用尺规作图法作出BC的垂直平分线DE,垂足为D,交AC于点E, (保留作图痕迹,不写作法);
(2)请用尺规作图法作出∠C的角平分线CF,交AB于点F,(保留作图痕迹,不写作法);
(3)请用尺规作图法在BC上找出一点P,使△PEF的周长最小.(保留作图痕迹,不写作法).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 是等边
是等边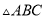 内一点,
内一点,  .将
.将 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 得
得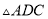 ,连接
,连接 .
.
(1)求证:
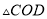 是等边三角形;
是等边三角形;(2)当
 时,试判断
时,试判断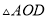 的形状,并说明理由;
的形状,并说明理由;(3)探究:当
 为多少度时,
为多少度时, 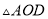 是等腰三角形?
是等腰三角形? -
科目: 来源: 题型:
查看答案和解析>>【题目】、在数轴上分别标出与下列各数最邻近的两个整数所对应的点的位置.
(1)
 ; (2)-
; (2)- ; (3)-
; (3)- ; (4)
; (4)  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察思考下列计算过程:
∵112=121,∴
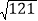 =
=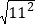 =11.
=11.同理,∵1112=12 321,∴
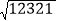 =
=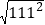 =111.
=111.由此你能猜想
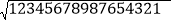 的值吗?总结规律并进行计算.
的值吗?总结规律并进行计算.
相关试题

