【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是 时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是 时,它们一定不全等.
参考答案:
【答案】钝角三角形或直角三角形,钝角三角形.
【解析】
试题分析:已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1.
证明:过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,则∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,在△BDC和△B1D1C1中,∵∠C=∠C1,∠BDC=∠B1D1C1,BC=B1C1,∴△BDC≌△B1D1C1,∴BD=B1D1,在Rt△BDA和Rt△B1D1A1中,∵AB=A1B1,BD=B1D1,∴Rt△BDA≌Rt△B1D1A1(HL),∴∠A=∠A1,在△ABC和△A1B1C1中,∵∠C=∠C1,∠A=∠A1,AB=A1B1,∴△ABC≌△A1B1C1(AAS).
同理可得:当这两个三角形都是钝角三角形或直角三角形时,它们也会全等,如图:△ACD与△ACB中,CD=CB,AC=AC,∠A=∠A,但:△ACD与△ACB不全等.
,故当这两个三角形其中一个三角形是锐角三角形,另一个是钝角三角形时,它们一定不全等.
故答案为:钝角三角形或直角三角形,钝角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在太阳光下行走,同一时刻他们的身高与其影长之比的关系是___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
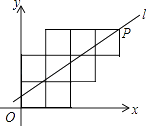
A.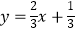
B.y= x+
x+ 
C.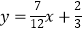
D.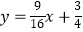
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市自2015年1月1日起对居民生活用电实行阶梯电价,具体收费标准如下表:

已知2016年10月份该市居民老李家用电200度,交电费120元;2016年9月份老李家交电费157元.
(1)表中a的值为;
(2)求老李家2016年9月份的用电量;
(3)若2016年8月份老李家用电的平均电价为0.7元/度,求老李家2016年8月份的用电量. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)10﹣(﹣5)+(﹣9)
(2)(﹣3)×(﹣9)+(﹣5)
(3)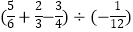
(4)﹣12014÷(﹣5)2×(﹣ )﹣|0.8﹣1|.
)﹣|0.8﹣1|. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,东生、夏亮两位同学从学校出发到青年路小学参加现场作文比赛,冬生步行一段时间后,夏亮骑自行车沿相同路线行进,两人都是匀速前进,他们的路程差s(米)与冬生出发时间t(分)之间的函数关系如图所示
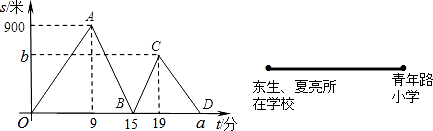
(提示:先根据图象还原东生、夏亮的行走过程,特别注意s代表的是两人的路程差)根据图象进行以下探究:
(1)冬生的速度是米/分,请你解释点B坐标(15,0)所表示的意义:;
(2)求夏亮的速度和他们所在学校与青年路小学的距离;
(3)求a,b值;
(4)线段CD对应的一次函数表达式中,一次项系数是多少?它的实际意义是什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(
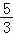 ,0),B(0,4),则点B2016的横坐标为( )
,0),B(0,4),则点B2016的横坐标为( )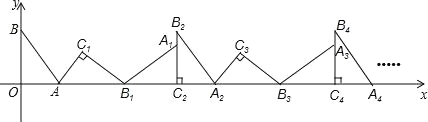
A.5 B.12 C.10070 D.10080
相关试题

