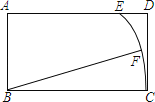
【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为 .
考点:全等三角形的判定与性质;角平分线的性质;矩形的性质;圆心角、弧、弦的关系;解直角三角形.
参考答案:
【答案】
【解析】
试题分析:连接CE交BF于H,连接BE,根据矩形的性质求出AB=CD=3,AD=BC=5=BE,∠A=∠D=90°,根据勾股定理求出AE=4,求出DE=1,根据勾股定理求出CE,求出CH,解直角三角形求出即可.
解:连接CE交BF于H,连接BE,
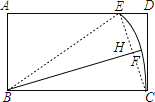
∵四边形ABCD是矩形,AB=3,BC=5,
∴AB=CD=3,AD=BC=5=BE,∠A=∠D=90°,
由勾股定理得:AE=![]() =4,DE=5﹣4=1,
=4,DE=5﹣4=1,
由勾股定理得:CE=![]() =
=![]() ,
,
由垂径定理得:CH=EH=![]() CE=
CE=![]() ,
,
在Rt△BFC中,由勾股定理得:BH=![]() =
=![]() ,
,
所以tan∠FBC=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的其中两边长分别为4,9,则这个等腰三角形的周长为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a3+a2=3a5
B.(3a)2=6a2
C.(a+b)2=a2+b2
D.2a2a3=2a5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.

(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:
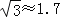 ,
,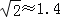 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果△ABC≌△DEF,△DEF的周长为13,DE=3,EF=4,则AC的长为( )
A. 13 B. 3 C. 4 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A. (﹣3a2)2=6a4 B. (﹣a3)2=﹣a6 C. (﹣x2)3=﹣x5 D. x3x2=x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个商店把某件商品按进价加20%作为定价,可是总卖不出去;后来老板按定价减价20%以96元出售,很快就卖掉了.则这次生意的盈亏情况为( )
A. 赚6元 B. 不亏不赚 C. 亏4元 D. 亏24元
相关试题

