【题目】在ABCD中,AE平分∠DAB交CD于E点、CF平分∠DCB交AB于点F.
(1)求证:四边形AECF是平行四边形;
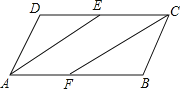
(2)若BG平分∠ABC交CD于G点,且AD=2EG=2,求四边形ABCD的周长.
参考答案:
【答案】(1)详见解析;(2)14或10.
【解析】
(1)由平行四边形的性质和角平分线的性质可得∠DEA=∠DCF,可证AE∥CF,即可得结论;
(2)分两种情况讨论,由角平分线的性质和平行四边形性质可求CD的长度,即可求四边形ABCD的周长.
证明:(1)∵四边形ABCD是平行四边形
∴AB∥CD,∠DAB=∠DCB
∵AE平分∠DAB交CD于E点、CF平分∠DCB交AB于点F.
∴∠DAE=∠EAB=![]() ∠DAB,∠DCF=∠BCF=
∠DAB,∠DCF=∠BCF=![]() ∠DCB,
∠DCB,
∴∠EAB=∠DCF
∵AB∥CD
∴∠DEA=∠EAB
∴∠DEA=∠DCF
∴AE∥CF,且AB∥CD
∴四边形AECF是平行四边形;
(2)如图,当点G在点E右侧,
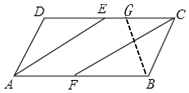
∵四边形ABCD是平行四边形
∴AB∥CD,AD=BC=2
∵AE平分∠DAB,
∴∠DAE=∠EAB
∵AB∥CD
∴∠DEA=∠EAB
∴∠AED=∠DAE
∴AD=DE=2,
同理可得:BC=GC=2
∵AD=2EG=2
∴EG=1
∴CD=DE+EG+GC=5
∴四边形ABCD的周长=2(AD+CD)=14
如图,若点G在点E左侧,

同理可得:DE=GC=2,GE=1
∴CD=DE+EC﹣GE=3
∴四边形ABCD的周长=2(AD+CD)=10
综上所述,四边形ABCD的周长为14或10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,点E在边CD上,点P在线段AE上,且到A、B、D三个顶点的距离分别为
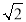 、2
、2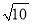 、6,则四边形BCDP的面积为_____.
、6,则四边形BCDP的面积为_____.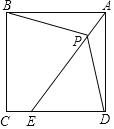
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知:a=
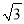 ﹣2,b=
﹣2,b=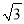 +2,求代数式a2b﹣ab2的值;
+2,求代数式a2b﹣ab2的值;(2)已知实数x、y满足x2+10x+
 +25=0,则(x+y)2019的值是多少?
+25=0,则(x+y)2019的值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为 ,CD的长为 ,AD的长为_____;
(3)△ACD为 三角形,四边形ABCD的面积为 .
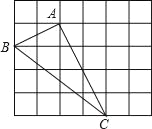
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A城气象台测得台风中心在A城正西方向240km的O处,以每小时30km的速度向南偏东60°的OB方向移动,距台风中心150km的范围内是受台风影响的区域.
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到台风的影响,求出受台风影响的时间有多长?
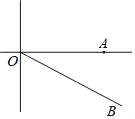
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,有四个同样大小的直角三角形,两条直角边分别为a、b,斜边为c,拼成一个正方形,中间留有一个小正方形.
(1)利用它们之间的面积关系,探索出关于a、b、c的等式;
(2)利用(1)中发现的直角三角形中两直角边a,b和斜边c之间的关系,完成问题:如图2,在直角△ABC中,∠C=90°,且c=6,a+b=8,则△ABC的面积为 ;
(3)如图3所示,CD是直角△ABC中斜边上的高,试证明CD2=ADBD.
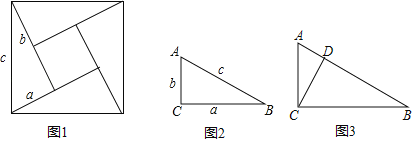
相关试题

