搜索
【题目】如图，某建筑物BC顶部有一旗杆AB，且点A，B，C在同一条直线上，小红在D处观测旗杆顶部A的仰角为47°，观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m，EC=21m，求旗杆AB的高度和建筑物BC的高度（结果保留小数后一位）．参考数据：tan47°≈1.07，tan42°≈0.90．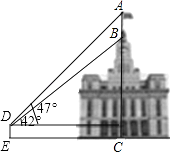
参考答案：
【答案】解：根据题意得DE=1.56，EC=21，∠ACE=90°，∠DEC=90°．
过点D作DF⊥AC于点F．
则∠DFC=90°∠ADF=47°，∠BDF=42°．
∵四边形DECF是矩形．
∴DF=EC=21，FC=DE=1.56，
在直角△DFA中，tan∠ADF= 
，
∴AF=DFtan47°≈21×1.07=22.47（m）．
在直角△DFB中，tan∠BDF= 
，
∴BF=DFtan42°≈21×0.90=18.90（m），
则AB=AF﹣BF=22.47﹣18.90=3.57≈3.6（m）．
BC=BF+FC=18.90+1.56=20.46≈20.5（m）．
答：旗杆AB的高度约是3.6m，建筑物BC的高度约是20.5米．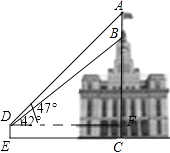
【解析】根据题意分别在两个直角三角形中求得AF和BF的长后求差即可得到旗杆的高度，进而求得BC的高度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一个直角三角形纸片ABO，放置在平面直角坐标系中，点A（
，0），点B（0，1），点0（0，0）．过边OA上的动点M（点M不与点O，A重合）作MN丄AB于点N，沿着MN折叠该纸片，得顶点A的对应点A′，设OM=m，折叠后的△AM′N与四边形OMNB重叠部分的面积为S．
（1）如图①，当点A′与顶点B重合时，求点M的坐标；
（2）如图②，当点A′，落在第二象限时，A′M与OB相交于点C，试用含m的式子表示S；
（3）当S=
时，求点M的坐标（直接写出结果即可）． -
科目： 来源： 题型：
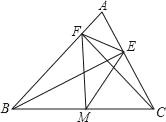
查看答案和解析>>【题目】如图，在△ABC中，CF⊥AB于F，BE⊥AC于E，M为BC的中点．
（1）若EF=3，BC=8，求△EFM的周长；
（2）若∠ABC=50°，∠ACB=60°，求∠EMF的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）的顶点为B（2，1），且过点A（0，2），直线y=x与抛物线交于点D，E（点E在对称轴的右侧），抛物线的对称轴交直线y=x于点C，交x轴于点G，EF⊥x轴，垂足为F，点P在抛物线上，且位于对称轴的右侧，PQ⊥x轴，垂足为点Q，△PCQ为等边三角形
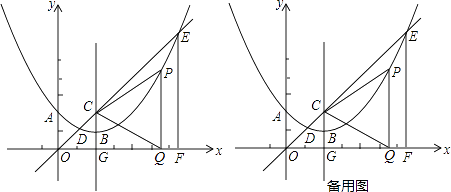
（1）求该抛物线的解析式；
（2）求点P的坐标；
（3）求证：CE=EF；
（4）连接PE，在x轴上点Q的右侧是否存在一点M，使△CQM与△CPE全等？若存在，试求出点M的坐标；若不存在，请说明理由．[注：3+2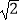
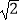=（ +1）2]． -
科目： 来源： 题型：
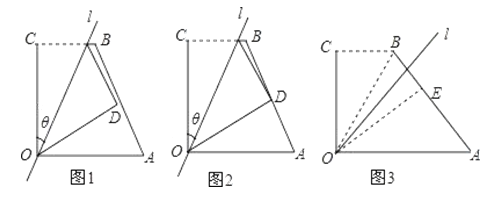
查看答案和解析>>【题目】（阅读）如图1，四边形OABC中，OA=a，OC=3，BC=2，∠AOC=∠BCO=90°，经过点O的直线l将四边形分成两部分，直线l与OC所成的角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ [θ，a ]
（理解）若点D与点A重合，则这个操作过程为FZ [45°，3]；
（尝试）
（1）若点D恰为AB的中点（如图2），求θ；
（2）经过FZ[45°，a]操作，点B落在点E处，若点E在四边形OABC的边AB上（如图3），求出a的值；若点E落在四边形OABC的外部，直接写出a的取值范围.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有两个构造完全相同（除所标数字外）的转盘A、B，游戏规定：转动两个转盘各一次，指向大的数字获胜．
（1）用树状图或列表格列出两个转盘转出的所有可能出现的结果；
（2）如果由你和小明各选择一个转盘游戏，你会选择哪一个，为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知反比例函数y=
与一次函数y=x+b的图形在第一象限相交于点A（1，﹣k+4）．
（1）试确定这两函数的表达式；
（2）求出这两个函数图象的另一个交点B的坐标，并求△AOB的面积；
（3）根据图象直接写出反比例函数值大于一次函数值的x的取值范围．
相关试题
