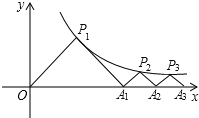
【题目】如图,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,点P1,P2,P3,…,Pn在函数y=![]() (x>0)的图象上,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上,则点A1的坐标是 ,点A2016的坐标是 .
(x>0)的图象上,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上,则点A1的坐标是 ,点A2016的坐标是 .
参考答案:
【答案】(2,0),(24![]() ,0).
,0).
【解析】
试题分析:分别作出点P1,P2,P3与x轴的垂线段,根据等腰直角三角形三线合一的性质可知,这此垂线段又是斜边上的中线,则等于斜边的一半;设未知数,根据反比例函数关系式列等量关系,求出未知数的值,并取舍,找出规律,并化简.
解:过点P1作P1B⊥x轴于B,
∵△P1OA1是等腰直角三角形,
∴OB=P1B,
则OBP1B=1,
∴OB=1,OA1=2,
∴A1(2,0);
过点P2作P2D⊥x轴于D,设A1D=x,则OD=2+x,
同理得:A1D=P2D=x,
则ODP2D=1,
x(2+x)=1,
解得:x1=﹣1+![]() ,x2=﹣1﹣
,x2=﹣1﹣![]() (舍),
(舍),
∴A2(2![]() ,0)
,0)
过点P3作P3E⊥x轴于E,设P3E=y,则OE=2![]() +y,
+y,
则OEP3E=1,
y(2![]() +y)=1,
+y)=1,
解得:y1=![]() ﹣
﹣![]() ,y2=﹣
,y2=﹣![]() (舍),
(舍),
∴A2A3=2![]() ﹣2
﹣2![]() ,
,
∴OA3=2![]() ﹣2
﹣2![]() +2
+2![]() =2
=2![]() ,
,
∴A3(2![]() ,0),
,0),
所以可以得出:A2016的坐标(2![]() ,0),即(24
,0),即(24![]() ,0),
,0),
故答案为:(2,0),(24![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点
 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当A点在反比例函数y=
 (x>0)的图象上移动时,B点坐标满足的反比例函数解析式为( )
(x>0)的图象上移动时,B点坐标满足的反比例函数解析式为( )
A.y=﹣
 (x<0) B.y=﹣
(x<0) B.y=﹣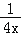 (x<0)
(x<0)C.y=﹣
 (x<0) D.y=﹣
(x<0) D.y=﹣ (x<0)
(x<0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )

A.(
 ,3)、(﹣
,3)、(﹣ ,4) B.(
,4) B.( ,3)、(﹣
,3)、(﹣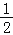 ,4)
,4)C.(
 ,
,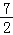 )、(﹣
)、(﹣ ,4) D.(
,4) D.( ,
,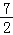 )、(﹣
)、(﹣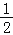 ,4)
,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).
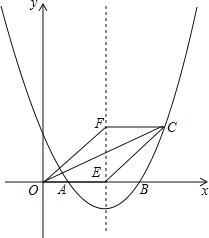
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形纸片ABCD中,AB=8,BC=20,F为BC的中点,沿过点F的直线翻折,使点B落在边AD上,折痕交矩形的一边于G,则折痕FG= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一次抛六枚均匀的骰子,朝上一面的点数都为6”这一事件是( )
A.必然事件
B.随机事件
C.确定事件
D.不可能事件
相关试题

