【题目】如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当A点在反比例函数y=![]() (x>0)的图象上移动时,B点坐标满足的反比例函数解析式为( )
(x>0)的图象上移动时,B点坐标满足的反比例函数解析式为( )

A.y=﹣![]() (x<0) B.y=﹣
(x<0) B.y=﹣![]() (x<0)
(x<0)
C.y=﹣![]() (x<0) D.y=﹣
(x<0) D.y=﹣![]() (x<0)
(x<0)
参考答案:
【答案】B
【解析】
试题分析:过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,设B点坐标满足的函数解析式是y=![]() ,易得△AOC∽△OBD,然后由相似三角形面积比等于相似比的平方,求得S△AOC:S△BOD=4,继而求得答案.
,易得△AOC∽△OBD,然后由相似三角形面积比等于相似比的平方,求得S△AOC:S△BOD=4,继而求得答案.
解:如图,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
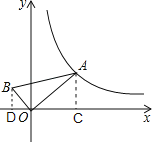
设B点坐标满足的函数解析式是y=![]() ,
,
∴∠ACO=∠BDO=90°,
∴∠AOC+∠OAC=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠BOD=∠OAC,
∴△AOC∽△OBD,
∴S△AOC:S△BOD=![]() ,
,
∵AO=2BO,
∴S△AOC:S△BOD=4,
∵当A点在反比例函数y=![]() (x>0)的图象上移动,
(x>0)的图象上移动,
∴S△AOC=![]() OCAC=
OCAC=![]() x
x![]() =
=![]() ,
,
∴S△BOD=![]() DOBD=
DOBD=![]() (﹣x
(﹣x![]() )=﹣
)=﹣![]() k,
k,
∴![]() =4×(﹣
=4×(﹣![]() k),解得k=﹣
k),解得k=﹣![]()
∴B点坐标满足的函数解析式y=﹣![]() (x<0).
(x<0).
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算结果是a8的值是( )
A.a2a4
B.a2+a6
C.(a2)4
D.a9﹣a -
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌自行车1月份销售量为100辆,每辆车售价相同.2月份的销售量比1月份增加10%,每辆车的售价比1月份降低了80元.2月份与1月份的销售总额相同,则1月份的售价为( )
A.880元 B.800元 C.720元 D.1080元
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点
 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )

A.(
 ,3)、(﹣
,3)、(﹣ ,4) B.(
,4) B.( ,3)、(﹣
,3)、(﹣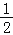 ,4)
,4)C.(
 ,
,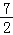 )、(﹣
)、(﹣ ,4) D.(
,4) D.( ,
,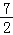 )、(﹣
)、(﹣ ,4)
,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,点P1,P2,P3,…,Pn在函数y=
 (x>0)的图象上,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上,则点A1的坐标是 ,点A2016的坐标是 .
(x>0)的图象上,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上,则点A1的坐标是 ,点A2016的坐标是 .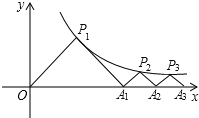
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).
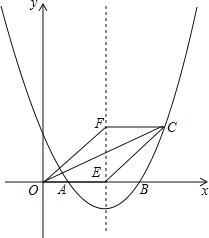
(1)求抛物线的解析式;
(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;
(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
相关试题

