【题目】由于数学课上需要用到科学计算器,班级决定集体购买,班长小明先去文具店购买了2个A型计算器和3个B型计算器,共花费90元;后又买了1个A型计算器和2个B型计算器,共花费55元(每次两种计算器的售价都不变)
(1)求A型计算器和B型计算器的售价分别是每个多少元?
(2)经统计,班内还需购买两种计算器共40个,设购买A型计算器t个,所需总费用w元,请求出w关于t的函数关系式;
(3)要求:B型计算器的数量不少于A型计数器的2倍,请设计一种购买方案,使所需总费用最低.
参考答案:
【答案】(1)A型计算器售价为每个15元,B型计算器售价为每个20元(2)W=-5t+800(3)购买A型计算器13个,B型计算器27个时,费用最低,最低费用为735元
【解析】试题分析:(1)设A型计算器的售价为每个x元,B型计算器的售价为每个y元,根据“购买了2个A型计算器和3个B型计算器,共花费90元,后又买了1个A型计算器和2个
B型计算器,共花费55元”,即可得到关于x、y的二元一次方程组,解之即可;
(2)设购买A型计算器t个,所需总费用w元,则买B型计算器(40-t)个,根据总价=单价×购买数量,即可得到w关于t的函数解析式;
(3)由B型计算器的数量不少于A型计数器的2倍,即可得出关于t的一元一次不等式,解之解可求出t的取值范围,再利用一次函数的性质可解决最值问题.
试题解析:(1)设A型计算机,售价为每个x元,b型计算机售价为每个为y元,根据
题意得: ![]() ,解得
,解得![]()
答:A型计算器售价为每个15元,B型计算器售价为每个20元
设购买A型计算机t个,所需总费用w元,则购买B型计算机(40-t)个
W=15t+20(40-t)=-5t+800
∵40-t≥2t,∴t≤![]()
W=-5t+800,∵-5<0,∴随t的增大而减小
∴t为整数,当t=13时,wmin=-5x13+800=735元
答:购买A型计算器13个,B型计算器27个时,费用最低,最低费用为735元
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次60秒跳绳测试中,10名同学跳的次数分别为170,190,180,150,180,180,160,200,180,190,则这次测试所跳次数的众数为
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣1)2015﹣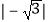 +
+ 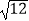 +(
+( 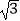 ﹣π)0;
﹣π)0;
(2)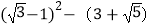
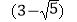
-
科目: 来源: 题型:
查看答案和解析>>【题目】如表记录的是今年宝应入冬以来连续四周的平均气温,请问周平均气温最低的是( )
记录周次
第一周
第二周
第三周
第四周
平均气温
3℃
0℃
-5℃
-2℃
A. 第一周B. 第二周C. 第三周D. 第四周
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(﹣2,a),(1,b)在直线y=2x+3上,则a_____b.(填“>”“<”或“=”号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三角形的两边长分别为3和4,则第三边的长不可能的是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
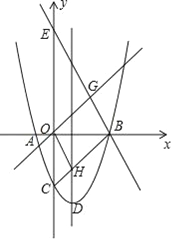
查看答案和解析>>【题目】如图,抛物线y=x2﹣(m+2)x+3(m﹣1)与x轴的两个交点为A、B,与y轴交于点C,点D为抛物线的顶点,直线y=﹣2x+m+6经过点B,交y轴于点E(0,6).
(1)求直线和抛物线的解析式;
(2)如果抛物线的对称轴与线段BC交于点H,且直线y=x与直线y=﹣2x+m+6交于点G,求证:四边形OHBG是平行四边形;
(3)在抛物线上是否存在点P,使△APB的面积等于平行四边形OHBG的面积,若存在,直接写出P点的坐标,若不存在请说明理由.
相关试题

