【题目】在正方形ABCD中,点E为BC边的中点,点B′与点B关于AE对称,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠ADB′=75°;④∠CB′D=135°.其中正确的是( )

A. ①② B. ①②④ C. ③④ D. ①②③④
参考答案:
【答案】B
【解析】分析:
(1)由轴对称的性质易得AB′=AB,结合AB=AD即可得到AB′=AD;
(2)连接B′E,易得BE=B′E=CE,由此易得∠BB′C=90°,由EF是△BB′C的中位线可得B′C=2EF,再证△B′EF∽△AB′F,可得![]() ,由此可得FB′=2FE,从而可得B′C=FB′,由此可得△FCB′为等腰直角三角形;
,由此可得FB′=2FE,从而可得B′C=FB′,由此可得△FCB′为等腰直角三角形;
(3)假设∠ADB′=75°成立,则可得∠AB′D=75°,由此可得∠ABB′=∠AB′B=60°,从而可得B′B=AB=BC,这与Rt△BB′C中B′B<BC矛盾,由此可得假设错误;
(4)由题意易得∠AB′D=∠ADB′,∠AB′B=∠ABB′,结合∠BAD=90°和四边形内角和为360°易得∠DB′B=135°,这样结合∠BB′C=90°可得∠DB′C=135°;
综上即可得到题中4个结论里正确的结论是①②④.
详解:
①∵点B′与点B关于AE对称,
∴△ABF与△AB′F关于AE对称,
∴AB=AB′,
∵AB=AD,
∴AB′=AD.故本选项正确;
②如图,连接EB′.

由题意可得:BE=B′E=EC,
∴∠FBE=∠FB′E,∠EB′C=∠ECB′,
∴∠FB′E+∠EB′C=∠FBE+∠ECB′=90°,
∴△BB′C为直角三角形.
∵FE为△BCB′的中位线,
∴B′C=2FE,
∵△B′EF∽△AB′F,
∴![]() ,即
,即![]() ,
,
∴FB′=2FE,
∴B′C=FB′,
∴△FCB′为等腰直角三角形.
故本选项正确.
③假设∠ADB′=75°成立,
则∠AB′D=75°,
∴∠ABB′=∠AB′B=360°-75°-75°-90°=60°,
∴△ABB′为等边三角形,
∴B′B=AB=BC,与B′B<BC矛盾,
故本选项错误.
④设∠ABB′=∠AB′B=x度,∠AB′D=∠ADB′=y度,
则在四边形ABB′D中,2x+2y+90=360,
∴x+y=135度.
又∵∠FB′C=90°,
∴∠DB′C=360°-135°-90°=135°.
故本选项正确.
故选B.
-
科目: 来源: 题型:
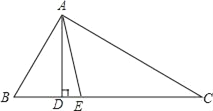
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,∠C=30°,AD和AE分别是△ABC的高和角平分线,求∠DAE的度数.
-
科目: 来源: 题型:
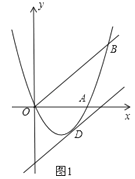
查看答案和解析>>【题目】如图1,已知抛物线y=ax2+bx(a≠0)经过A(6,0)、B(8,8)两点.
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
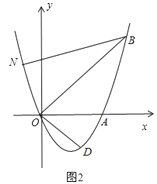
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,在坐标平面内有点P,求出所有满足△POD∽△NOB的点P坐标(点P、O、D分别与点N、O、B对应).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,BA=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
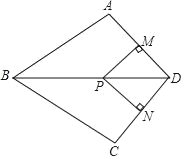
(1)求证:点A与C关于直线BD对称.
(2)若∠ADC=90°,求证四边形MPND为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆O的直径,以AO为直径作半圆M,C为OB的中点,D在半圆M上,且CD⊥MD,延长AD交半圆O于点E,且AB=4,则圆中阴影部分的面积为_____________.
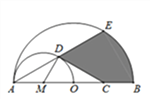
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
阅读理解:数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用较大数与较小数的差来表示.例如:
在数轴上,有理数3与1对应的两点之间的距离为
 ;
;在数轴上,有理数3与-2对应的两点之间的距离为
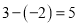 ;
;在数轴上,有理数-3与-2对应的两点之间的距离为
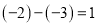 .
.解决问题:如图所示,已知点
 表示的数为-3,点
表示的数为-3,点 表示的数为-1,点
表示的数为-1,点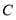 表示的数为2.
表示的数为2.
(1)点
 和点
和点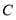 之间的距离为______.
之间的距离为______.(2)若数轴上动点
 表示的数为
表示的数为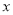 ,当
,当 时,点
时,点 和点
和点 之间的距离可表示为______;当
之间的距离可表示为______;当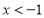 时,点
时,点 和点
和点 之间的距离可表示为______.
之间的距离可表示为______.(3)若数轴上动点
 表示的数为
表示的数为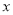 ,点
,点 在点
在点 和点
和点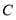 之间,点
之间,点 和点
和点 之间的距离表示为
之间的距离表示为 ,点
,点 和点
和点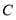 之间的距离表示为
之间的距离表示为 ,求
,求 (用含
(用含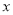 的代数式表示并进行化简)
的代数式表示并进行化简)(4)若数轴上动点
 表示的数为-2,将点
表示的数为-2,将点 向右移动19个单位长度,再向左移动23个单位长度终点为
向右移动19个单位长度,再向左移动23个单位长度终点为 ,那么
,那么 ,
, 两点之间的距离是______.
两点之间的距离是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中点
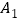 的坐标为(1,0),过点
的坐标为(1,0),过点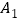 作x轴的垂线交直线y=2x于
作x轴的垂线交直线y=2x于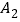 ,过点
,过点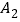 作直线y=2x的垂线交x轴于
作直线y=2x的垂线交x轴于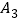 ,过点
,过点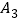 作x轴的垂线交直线y=2x于
作x轴的垂线交直线y=2x于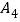 …,依此规律,则
…,依此规律,则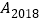 的坐标为___________.
的坐标为___________.
相关试题

