【题目】现有若干张如图1所示的正方形纸片A,B和长方形纸片C.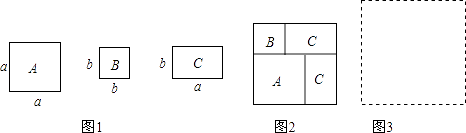
(1)小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式:;
(2)小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是 , 并请你在图3位置画出拼成的长方形;
(3)根据拼图经验,请将多项式a2+5ab+4b2分解因式.
参考答案:
【答案】
(1)a2+2ab+b2=(a+b)2
(2)2;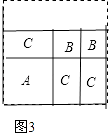
(3)
a2+5ab+4b2=(a+b)(a+4b).
【解析】解:(1)利用面积相等得a2+2ab+b2=(a+b)2;(2)由于有a2+3ab,则a2+3ab+nb2分解为(a+b)(a+2b),因此得到n=2,
如图:
【考点精析】解答此题的关键在于理解因式分解的应用的相关知识,掌握因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
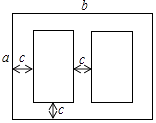
(1)用代数式表示这两个篮球场的占地面积.
(2)当a=30,b=40,c=3时,计算出一个篮球场的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC,点D为射线BC上一个动点(不与B、C重合),以AD为一边向AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线,交直线AB于点F,连接BE.
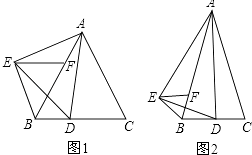
(1)如图1,若∠BAC=∠DAE=60°,判断△BEF的形状并说明理由.
(2)若∠BAC=∠DAE≠60°如图2,当点D在线段BC上移动,判断△BEF的形状,不必说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=2x﹣1,当自变量x增加a时,则函数值y增加_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,过点(﹣2,3)的直线l经过一、二、三象限,若点(0,a),(﹣1,b),(c,﹣1)都在直线l上,则下列判断正确的是( )
A.a<b
B.a<3
C.b<3
D.c<﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】据民政部网站消息截至2018年底,我国60岁以上老年人口巳经达到2.56亿人。其中2.56 亿用科学记数法表示为( )
A. 2.56×107 B. 2.56×108 C. 2.56×l09 D. 2.56×l010
-
科目: 来源: 题型:
查看答案和解析>>【题目】若y=(m+2)x|m|﹣1是正比例函数.(1)求m的值m=_____;(2)关系式是_____.
相关试题

