【题目】△ABC中,AB=AC,点D为射线BC上一个动点(不与B、C重合),以AD为一边向AD的左侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作BC的平行线,交直线AB于点F,连接BE. 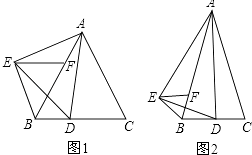
(1)如图1,若∠BAC=∠DAE=60°,判断△BEF的形状并说明理由.
(2)若∠BAC=∠DAE≠60°如图2,当点D在线段BC上移动,判断△BEF的形状,不必说明理由
参考答案:
【答案】
(1)解:△BEF为等边三角形,
∵AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴△AED和△ABC为等边三角形,
∴∠C=∠ABC=60°,∠EAB=∠DAC,
∴△EAB≌△DAC,
∴∠EBA=∠C=60°,
∵EF∥BC,
∴∠EFB=∠ABC=60°,
∵在△EFB中,∠EFB=∠EBA=60°,
∴△EFB为等边三角形
(2)解:根据(1)的证明可知,
∠EBA=∠C,∠EFB=∠ABC,
∴△BEF为等腰三角形
【解析】(1)根据已知证明△EAB≌△DAC,得到∠EBA=∠C=60°,根据EF∥BC,得到∠EFB=∠ABC=60°,证明结论;(2)与(1)的证明过程类似,可以得到答案.
【考点精析】根据题目的已知条件,利用等腰三角形的判定和等边三角形的判定的相关知识可以得到问题的答案,需要掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(3x+4)(3x﹣4)﹣x(x﹣4)>8(x+1)2 , 并把它的解集在数轴上表示出来.
-
科目: 来源: 题型:
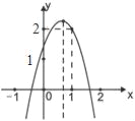
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
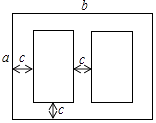
(1)用代数式表示这两个篮球场的占地面积.
(2)当a=30,b=40,c=3时,计算出一个篮球场的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=2x﹣1,当自变量x增加a时,则函数值y增加_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有若干张如图1所示的正方形纸片A,B和长方形纸片C.
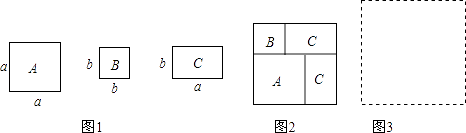
(1)小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式:;
(2)小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是 , 并请你在图3位置画出拼成的长方形;
(3)根据拼图经验,请将多项式a2+5ab+4b2分解因式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,过点(﹣2,3)的直线l经过一、二、三象限,若点(0,a),(﹣1,b),(c,﹣1)都在直线l上,则下列判断正确的是( )
A.a<b
B.a<3
C.b<3
D.c<﹣2
相关试题

