【题目】杨辉是我国南宋时期杰出的数学家和教育家,下图是杨辉在公元1261年著作《详解九章算法》里面的一张图,即“杨辉三角”,该图中有很多规律,请仔细观察,解答下列问题: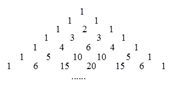
(1)图中给出了七行数字,根据构成规律,第8行中从左边数第3个数是;
(2)利用不完全归纳法探索出第n行中的所有数字之和为 .
参考答案:
【答案】
(1)21
(2)![]()
【解析】解:(1) 设第n行第2个数为 ![]() (n≥2,n为正整数),第n行第3个数为
(n≥2,n为正整数),第n行第3个数为 ![]() b(n≥3,n为正整数),观察,发现规律:
b(n≥3,n为正整数),观察,发现规律:
∵ ![]() =1,
=1, ![]() =2,
=2, ![]() =3,
=3, ![]() =4,
=4, ![]() =5,
=5,
∴ ![]() =n1;
=n1;
∵ ![]() =1,
=1, ![]() =3=1+2=
=3=1+2= ![]() +2,
+2, ![]() =6=3+3=
=6=3+3= ![]() +3,
+3, ![]() =10=6+4=
=10=6+4= ![]() +4,…,
+4,…,
∴ ![]()
![]() =n2,
=n2,
∴ ![]() =
= ![]() +
+ ![]()
![]() +
+ ![]()
![]() +
+ ![]() -
- ![]() +…+
+…+ ![]()
![]() =1+2+3+…+n2=
=1+2+3+…+n2= ![]() .
.
当n=8时, ![]() =
= ![]() =21.
=21.
⑵第一行数字之和1= ![]() ,第二行数字之和2=
,第二行数字之和2= ![]() ,第三行数字之和4=
,第三行数字之和4= ![]() ,第四行数字之和8=
,第四行数字之和8= ![]() ,…∴第n行数字之和为
,…∴第n行数字之和为 ![]() ,
,
本题主要考查数字的变化类,解题的关键是每行的数相加,分析总结得出规律,根据规律求出第n行的数据之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,用量角器度量几个角的度数,下列结论中正确的是( )
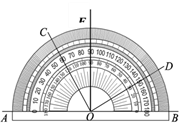
A.∠BOC=60°
B.∠COA是∠EOD 的余角
C.∠AOC=∠BOD
D.∠AOD与∠COE互补 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB.
(1)求证:DE与⊙O相切;
(2)若∠C=30°,求∠BOD的度数;
(3)在(2)的条件下,若⊙O半径为2, 求阴影部分面积.
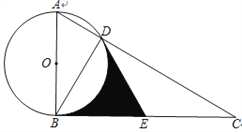
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD , E 是CB 延长线上一点,下列推理正确的是( )

A.如果∠1=∠2 ,那么AB∥CD
B.如果∠3=∠4 ,那么 AD∥BC
C.如果AD∥BC , 那么∠6+∠BAD=180°.
D.如果∠6+∠BCD=180°,那么AD∥BC -
科目: 来源: 题型:
查看答案和解析>>【题目】若ab=3,a﹣2b=5,则a2b﹣2ab2的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内,⊙O的半径为1,点P到O的距离为2,过点P可作⊙O的切线条数为( )
A. 0条B. 1条C. 2条D. 无数条
-
科目: 来源: 题型:
查看答案和解析>>【题目】在3×3的方格纸中,点A,B,C,D,E分别位于如图所示的小正方形格点上.
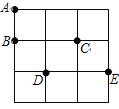
(1)在点A,B,C,D,E中任取四个点为顶点直接在图上画一个中心对称的四边形;
(2)从A,B,C三个点中先任取一个点,在余下的两个点中再取一个点,将所取的这两点与点D,E为顶点构成四边形,求所得四边形中面积为2的概率(用树状图或列表法求解).
相关试题

