搜索
【题目】若关于x的分式方程 
无解，则m的值为_______．
【答案】-4，-6
【解析】试题分析：去分母得：x(m＋2x)－2x(x－3)＝2(x－3)，
(m＋4)x＝－6，
当m＋4≠0时，
x＝
≠0，
∵分式方程无解，
∴x－3＝
－3＝0，
解得：m＝－6；
当m＋4＝0即m＝－4时，
整式方程无解，分式方程也无解，符合题意，
故m的值为－4或－6．
故答案为：－4或－6．
【题型】填空题
【结束】
19
【题目】计算:
（1）
(2) 
(3) 
(4) 
参考答案：
【答案】(1) 
;(2) 
;(3) 
; (4) 
【解析】试题分析：（1）分子、分母分解因式后约分即可；
（2）先通分计算括号内分式的减法，然后把除法转化为乘法，分子、分母分解因式后约分即可；
（3）第二个分式分子、分母分解因式后约分，然后通分转化为同分母分式，最后依照同分母分式的加减法则计算即可；
（4）先通分计算括号内分式的减法，然后把除法转化为乘法，分子、分母分解因式后约分即可．
试题解析：
解：（1）原式＝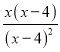
＝
；
（2）原式＝
＝
＝
；
（3）原式＝
＝
＝
＝
＝
；
（4）原式＝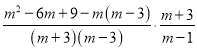
＝
＝
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的分式方程
=1的解是正数，则m的取值范围是_____．【答案】m＜1
【解析】试题分析：去分母得：2x＋m＝x－2，
解得：x＝－m－2，
∵关于x的方程
＝1的解是正数，∴－m－2＞0，
解得m＜－2，
又∵x＝－m－2≠2，
∴m≠－4，
∴m的取值范围是：m＜－2且m≠－4．
故答案为：m＜－2且m≠－4．
点睛：此题主要考查了分式方程的解，要熟练掌握，解答此题的关键是要明确：在解方程的过程中因为在把分式方程化为整式方程的过程中，扩大了未知数的取值范围，可能产生增根，增根是令分母等于0的值，不是原分式方程的解．
【题型】填空题
【结束】
18【题目】若关于x的分式方程
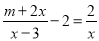无解，则m的值为_______． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC．
（1）判断直线l与⊙O的位置关系，并说明理由；
（2）若∠ABC的平分线BF交AD于点F，求证：BE=EF；
（3）在（2）的条件下，若DE=4，DF=3，求AF的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．
求证：中点四边形EFGH是平行四边形；
（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明） -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读后回答问题：
计算(－
)÷(－15)×(－
)解：原式＝－
÷[(－15)×(－)] ①＝－
÷1 ②＝－
③（）上述的解法是否正确？答：_________________________
若有错误，在哪一步？答：_________________________（填代号）
错误的原因是：___________________________________
（2）这个计算题的正确答案应该是：______________________
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算:
（1）
(2) 
(3)
(4) 
【答案】(1)
;(2) 
;(3) 
; (4) 
【解析】试题分析：（1）分子、分母分解因式后约分即可；
（2）先通分计算括号内分式的减法，然后把除法转化为乘法，分子、分母分解因式后约分即可；
（3）第二个分式分子、分母分解因式后约分，然后通分转化为同分母分式，最后依照同分母分式的加减法则计算即可；
（4）先通分计算括号内分式的减法，然后把除法转化为乘法，分子、分母分解因式后约分即可．
试题解析：
解：（1）原式＝
＝
；（2）原式＝
＝
＝
；（3）原式＝
＝
＝
＝
＝
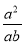
；（4）原式＝
＝
＝
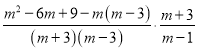
．点睛：此题考查了分式的混合运算，熟练掌握运算法则和运算顺序是解本题的关键．
【题型】解答题
【结束】
20【题目】解分式方程：
(1)
(2) 
-
科目： 来源： 题型：
查看答案和解析>>【题目】解分式方程：
(1)
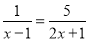(2) 
【答案】(1)
;(2)x=
【解析】试题分析：（1）两边乘以(x－1)(2x＋1)去分母，转化为整式方程，然后解整式方程，检验后写出分式方程的解即可；
（2）两边乘以(x＋2)(x－2)去分母，转化为整式方程，然后解整式方程，检验后写出分式方程的解即可．
试题解析：
解：（1）两边乘以(x－1)(2x＋1)去分母得：2x＋1＝5(x－1)，
解得：x＝2，
当x＝2时，(x－1)(2x＋1)≠0，
∴原分式方程的解为x＝2；
（2）两边乘以(x＋2)(x－2)去分母得：(x－2)2－3＝(x＋2)(x－2)，
解得：x＝
，当x＝
时，(x＋2)(x－2)≠0，所以原分式方程的解为x＝
．【题型】解答题
【结束】
21【题目】先化简，再求值
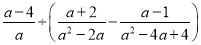，其中
的值从不等式组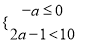
的整数解中选取.
相关试题
