【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
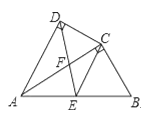
(1)求证:AC2=AB![]() AD;
AD;
(2)求证:CE∥AD;
(3)若AD=5,AB=7,求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=AB![]() AD;
AD;
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=![]() AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得![]() 的值.
的值.
试题解析: (1)∵AC平分∠DAB,
∴∠DAC=∠CAB.
又∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB.
∴AD:AC=AC:AB,
∴AC2=AB![]() AD.
AD.
(2)∵E为AB的中点,∠ACB=90°,
∴CE=![]() AB=AE.
AB=AE.
∴∠EAC=∠ECA.
∵∠DAC=∠CAB,
∴∠DAC=∠ECA.
∴AD∥CE;
(3)∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=![]() AB,
AB,
∴CE=![]() ×7=
×7=![]() ,
,
∵AD=5,
∴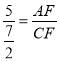 ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. 0既不是正数,也不是负数
B. 1是绝对值最小的数
C. 一个有理数不是整数就是分数
D. 0的绝对值是0
-
科目: 来源: 题型:
查看答案和解析>>【题目】_______的算数平方根是它本身.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
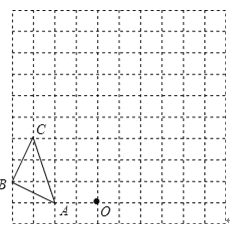
(1)把△ABC绕点O顺时针旋转90°得到△A1B1C1;
(2)以图中的O为位似中心,在△A1B1C1的同侧将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
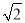 ≈1.41,
≈1.41,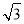 ≈1.73)
≈1.73)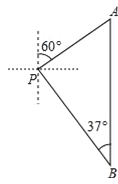
-
科目: 来源: 题型:
查看答案和解析>>【题目】向东走5m,记为+5m,那么走﹣10m,表示( )
A. 向西走10m B. 向东走10m C. 向南走10m D. 向北走10m
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店上月的营业额是a万元,本月比上月增长15%,则本月营业额是( )
A. 15%(a+1)万元 B. 15% a万元 C. (1+15%)a万元 D. (1+15%)2a万元
相关试题

