【题目】如图所示,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(﹣1,1),点C的坐标为(﹣4,2),则这两个正方形位似中心的坐标是 . 
参考答案:
【答案】(2,0)或(﹣ ![]() ,
, ![]() )
)
【解析】解:①当两个位似图形在位似中心同旁时,位似中心就是CF与x轴的交点, 设直线CF解析式为y=kx+b,将C(﹣4,2),F(﹣1,1)代入,得 ![]() ,
,
解得 ![]() 即y=﹣
即y=﹣ ![]() x+
x+ ![]() ,
,
令y=0得x=2,
∴O′坐标是(2,0);
②当位似中心O′在两个正方形之间时,
可求直线OC解析式为y=﹣ ![]() x,直线DE解析式为y=
x,直线DE解析式为y= ![]() x+1,
x+1,
联立 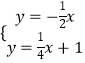 ,解得
,解得 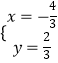 ,
,
即O′(﹣ ![]() ,
, ![]() ).
).
所以答案是:(2,0)或(﹣ ![]() ,
, ![]() ).
).
【考点精析】认真审题,首先需要了解位似变换(它们具有相似图形的性质外还有图形的位置关系(每组对应点所在的直线都经过同一个点—位似中心)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在矩形ABCD中,AB=
 ,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( )
,BC=2,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是( ) 
A.
B.
C.1
D.1.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在梯形ABCD中,AB∥CD,E是BC的中点,EF⊥AD于点F,AD=4,EF=5,则梯形ABCD的面积是( )

A.40
B.30
C.20
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速(精确到0.1秒)?(参考数据:
 ≈1.41,
≈1.41,  ≈1.73,60千米/时=
≈1.73,60千米/时=  米/秒)
米/秒) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6cm,∠ABC=60°,则四边形ABCD的面积等于cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个全等的等腰直角三角板(斜边长为2)如图放置,其中一块三角板45°角的顶点与另一块三角板ABC的直角顶点A重合.若三角板ABC固定,当另一个三角板绕点A旋转时,它的直角边和斜边所在的直线分别与边BC交于点E、F.设BF=x,CE=y,则y关于x的函数图象大致是( )

A.
B.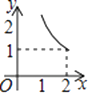
C.
D.
相关试题

