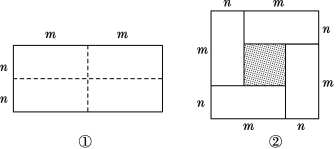
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀把它均分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)你认为图②中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图②中阴影部分的面积.
(3)观察图②你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,mn.
(4)根据(3)题中的等量关系,解决如下问题:
已知a+b=7,ab=5,求(a-b)2的值.(写出过程)
参考答案:
【答案】解:(1)m-n;(2)详见解析;(3)(m+n)2=(m-n)2+4mn;(4)29.
【解析】
(1)观察可得阴影部分的正方形边长是m-n;
(2)方法1:边长为m+n的大正方形的面积减去4个长为m,宽为n的小长方形面积;
方法2:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积;
(3)由(2)可得结论(m+n)2=(m-n)2+4mn;
(4)由(a-b)2=(a+b)2-4ab求解.
(1)阴影部分的正方形边长是m-n.
(2)阴影部分的面积就等于边长为m-n的小正方形的面积,
方法1:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,
即(m-n)2=(m+n)2-4mn;
方法2:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,
即(m-n)2=(m+n)2-2m2n=(m+n)2-4mn;
(3)(m+n)2=(m-n)2+4mn.
(4)(a-b)2=(a+b)2-4ab=49-4×5=29.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举行春季运动会,需要在初三年级选取1或2名同学作为志愿者,初三(5)班的小熊、小乐和初三(6)班的小矛、小管4名同学报名参加.
(1)若从这4名同学中随机选取1名志愿者,则被选中的这名同学恰好是初三(5)班同学的概率是;
(2)若从这4名同学中随机选取2名志愿者,请用列举法(画树状图或列表)求这2名同学恰好都是初三(6)班同学的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy,直线y=x﹣1与y轴交于点A,与双曲线y=
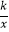 交于点B(m,2).
交于点B(m,2).
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若△ABC的面积为6,求直线CD的表达式. -
科目: 来源: 题型:
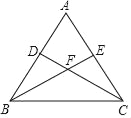
查看答案和解析>>【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-23+
 (2 018+3)0-
(2 018+3)0-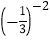 ;(2)
;(2)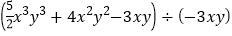 ;
;(3)(-2+x)(-2-x); (4)(a+b-c)(a-b+c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别是(-3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造PCOD.在线段OP延长线上一动点E,且满足PE=AO.
(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;
(2)当点P运动的时间为
 秒时,求此时四边形ADEC的周长是多少.
秒时,求此时四边形ADEC的周长是多少.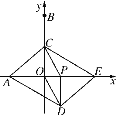
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次篮球联赛初赛阶段,每队有
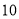 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得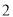 分, 负一场得
分, 负一场得 分,积分超过
分,积分超过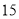 分才能获得参赛资格.
分才能获得参赛资格.(1)已知甲队在初赛阶段的积分为
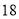 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
相关试题

