【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .

参考答案:
【答案】3或6.
【解析】当△CEB′为直角三角形时,有两种情况:
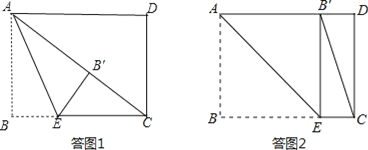
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=6,BC=8,
∴AC=![]() =10,
=10,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,如图,
∴EB=EB′,AB=AB′=6,
∴CB′=10﹣6=4,
设BE=x,则EB′=x,CE=8﹣x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+42=(8﹣x)2,
解得x=3,
∴BE=3;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,
∴BE=AB=6.
综上所述,BE的长为3或6.
故答案为:3或6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)已知二次函数y=ax2+bx+1的图象经过点(1,3)和(3,﹣5),求a、b的值;
(2)已知二次函数y=﹣x2+bx+c的图象与x轴的两个交点的横坐标分别为1和2.求这个二次函数的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知 A (-4,n), B (2,-4)是一次函数 y=kx+b的图象和反比例函数
 的图象的两个交点.
的图象的两个交点. 
(1)求反比例函数和一次函数的关系式;
(2)求直线 AB 与 x 轴的交点 C 的坐标及△ AOB 的面积;
(3)求方程 kx+b-
 =0的解(请直接写出答案);
=0的解(请直接写出答案); (4)求不等式 kx+b-
 <0的解集(请直接写出答案).
<0的解集(请直接写出答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】学习有理数的乘法后,老师给同学们这样一道题目:计算:49
 ×(﹣5),看谁算的又快又对,有两位同学的解法如下:
×(﹣5),看谁算的又快又对,有两位同学的解法如下: 小明:原式=﹣
 ×5=﹣
×5=﹣ =﹣249
=﹣249 ;
; 小军:原式=(49+
 )×(﹣5)=49×(﹣5)+
)×(﹣5)=49×(﹣5)+ ×(﹣5)=﹣249
×(﹣5)=﹣249 ;
; (1)对于以上两种解法,你认为谁的解法较好?
(2)上面的解法对你有何启发,你认为还有更好的方法吗?如果有,请把它写出来;
(3)用你认为最合适的方法计算:19
 ×(﹣8)
×(﹣8) -
科目: 来源: 题型:
查看答案和解析>>【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).

(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;
(2)以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的中线AF与中位线DE相交于点O。
(1)AF与DE有怎样的关系?为什么?
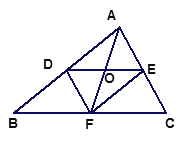
(2)当△ABC满足什么条件时,四边形DFEA是菱形?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数
空间与图形
统计与概率
综合与实践
学生甲
90
93
89
90
学生乙
94
92
94
86
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
相关试题

