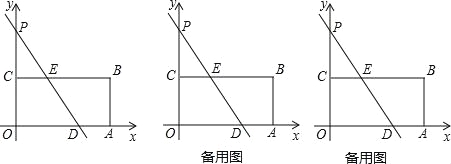
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=﹣![]() x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣![]() x+b平分矩形OABC的面积,求b的值;
x+b平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,当直线y=﹣![]() x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
(3)在(1)的条件下,将矩形OABC沿DE折叠,若点O落在边BC上,求出该点坐标;若不在边BC上,求将(1)中的直线沿y轴怎样平移,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
参考答案:
【答案】(1)b=12;(2)存在,DM=8﹣![]() 或DM=8+
或DM=8+![]() ;(3)沿y轴向下平移
;(3)沿y轴向下平移![]() 个单位,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
个单位,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
【解析】
试题分析:(1)根据直线y=﹣![]() x+b平分矩形OABC的面积,知道其必过矩形的中心,然后求得矩形的中心坐标为(6,3),代入解析式即可求得b值;(2)假设存在ON平分∠CNM的情况,分当直线PM与边BC和边OA相交和当直线PM与直线BC和x轴相交这两种情况,求得DM的值就存在,否则就不存在;
x+b平分矩形OABC的面积,知道其必过矩形的中心,然后求得矩形的中心坐标为(6,3),代入解析式即可求得b值;(2)假设存在ON平分∠CNM的情况,分当直线PM与边BC和边OA相交和当直线PM与直线BC和x轴相交这两种情况,求得DM的值就存在,否则就不存在;
(3)假设沿DE将矩形OABC折叠,点O落在边BC上O′处,连接PO′、OO′,得到△OPO′为等边三角形,从而得到∠OPD=30°,然后根据(2)知∠OPD>30°,得到沿DE将矩形OABC折叠,点O不可能落在边BC上;若设沿直线y=﹣![]() x+a将矩形OABC折叠,点O恰好落在边BC上O′处,连接P′O′、OO′,则有P′O′=OP′=a,在Rt△OPD和Rt△OAO′中,利用正切的定义求得a值,即可得到将矩形OABC沿直线折叠,点O恰好落在边BC上,于是得到问题的答案.
x+a将矩形OABC折叠,点O恰好落在边BC上O′处,连接P′O′、OO′,则有P′O′=OP′=a,在Rt△OPD和Rt△OAO′中,利用正切的定义求得a值,即可得到将矩形OABC沿直线折叠,点O恰好落在边BC上,于是得到问题的答案.
试题解析:(1)∵直线y=﹣![]() x+b平分矩形OABC的面积,∴其必过矩形的中心,由题意得矩形的中心坐标为(6,3),∴3=﹣
x+b平分矩形OABC的面积,∴其必过矩形的中心,由题意得矩形的中心坐标为(6,3),∴3=﹣![]() ×6+b,解得b=12;(2)假设存在ON平分∠CNM的情况,①当直线PM与边BC和边OA相交时,过O作OH⊥PM于H,∵ON平分∠CNM,OC⊥BC,∴OH=OC=6,由(1)知OP=12,∴∠OPM=30°,∴OM=OPtan30°=
×6+b,解得b=12;(2)假设存在ON平分∠CNM的情况,①当直线PM与边BC和边OA相交时,过O作OH⊥PM于H,∵ON平分∠CNM,OC⊥BC,∴OH=OC=6,由(1)知OP=12,∴∠OPM=30°,∴OM=OPtan30°=![]() ,当y=0时,由﹣
,当y=0时,由﹣![]() x+12=0解得x=8,∴OD=8,∴DM=8﹣
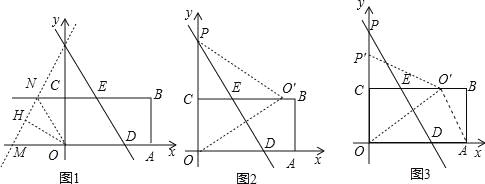
x+12=0解得x=8,∴OD=8,∴DM=8﹣![]() ;②如图1,当直线PM与直线BC和x轴相交时,同上可得OM=
;②如图1,当直线PM与直线BC和x轴相交时,同上可得OM=![]() ,OD=8,∴DM=8+
,OD=8,∴DM=8+![]() .所以存在ON平分∠CNM的情况,DM=8﹣
.所以存在ON平分∠CNM的情况,DM=8﹣![]() 或DM=8+
或DM=8+![]() ;(3)如图2假设沿DE将矩形OABC折叠,点O落在边BC上O′处连接PO′、OO′,则有PO′=OP,又由(1)得BC垂直平分OP,∴PO′=OO′,∴△OPO′为等边三角形,∴∠OPD=30°,而由(2)知∠OPD>30°,所以沿DE将矩形OABC折叠,点O不可能落在边BC上;如图3设沿直线y=﹣
;(3)如图2假设沿DE将矩形OABC折叠,点O落在边BC上O′处连接PO′、OO′,则有PO′=OP,又由(1)得BC垂直平分OP,∴PO′=OO′,∴△OPO′为等边三角形,∴∠OPD=30°,而由(2)知∠OPD>30°,所以沿DE将矩形OABC折叠,点O不可能落在边BC上;如图3设沿直线y=﹣![]() x+a将矩形OABC折叠,点O恰好落在边BC上O′处,连接P′O′、OO′,则有P′O′=OP′=a,由题意得:CP′=a﹣6,∠OPD=∠CO′O,在Rt△OPD中,tan∠OPD=
x+a将矩形OABC折叠,点O恰好落在边BC上O′处,连接P′O′、OO′,则有P′O′=OP′=a,由题意得:CP′=a﹣6,∠OPD=∠CO′O,在Rt△OPD中,tan∠OPD=![]() ,在Rt△OCO′中,tan∠CO′O=
,在Rt△OCO′中,tan∠CO′O=![]() ,∴
,∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得CO′=9,在Rt△CP′O′中,由勾股定理得:(a﹣6)2+92=a2,解得a=
,解得CO′=9,在Rt△CP′O′中,由勾股定理得:(a﹣6)2+92=a2,解得a=![]() ,12﹣
,12﹣![]() =
=![]() ,所以将直线y=﹣
,所以将直线y=﹣![]() x+12沿y轴向下平移
x+12沿y轴向下平移![]() 个单位得直线y=﹣
个单位得直线y=﹣![]() x+
x+![]() ,将矩形OABC沿直线y=﹣
,将矩形OABC沿直线y=﹣![]() x+
x+![]() 折叠,点O恰好落在边BC上.
折叠,点O恰好落在边BC上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AE⊥AB且AE=AB,BC⊥CD且BC=CD,按照图中所标注的数据,则图中阴影部分图形的面积S等于( )

A. 50 B. 62 C. 65 D. 68
-
科目: 来源: 题型:
查看答案和解析>>【题目】点B(3,-2)到x轴的距离是_________;到y轴的距离是____________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
一般地,n个相同的因数a相乘
 记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).(1)计算:log28=______;
(2)计算:
 ;
;(3)log55、log525、log5125之间满足怎样的关系式,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上表示﹣3的点在原点的_____侧,距离原点_____个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,G是BC上任意一点,连结AG,DE⊥AG于点E,BF∥DE交AG于点F,探究线段DE,BF,EF三者之间的数量关系,并说明理由.

相关试题

