【题目】某物流公司承接A,B两种货物运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨;该物流公司6月承接的A种货物和B种数量与5月份相同,6月份共收取运费13000元.
(1)该物流公司月运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收到多少运输费?
参考答案:
【答案】
(1)解:设A种货物运输了x吨,设B种货物运输了y吨,
依题意得: ![]() ,
,
解之得: ![]() .
.
答:物流公司月运输A种货物100吨,B种货物150吨
(2)解:设A种货物为a吨,则B种货物为(330﹣a)吨,
依题意得:a≤(330﹣a)×2,
解得:a≤220,
设获得的利润为W元,则W=70a+40(330﹣a)=30a+13200,
根据一次函数的性质,可知W随着a的增大而增大
当W取最大值时a=220,
即W=19800元.
所以该物流公司7月份最多将收到19800元运输费
【解析】)(1)设A种货物运输了x吨,设B种货物运输了y吨,由已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元和6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨;该物流公司6月承接的A种货物和B种数量与5月份相同,6月份共收取运费13000元.得出方程组求解即可;(2)设A种货物为a吨,则B种货物为(330﹣a)吨,依题意得:a≤(330﹣a)×2,找到a的取值范围,设获得的利润为W元,则W=70a+40(330﹣a)=30a+13200,根据一次函数的性质,可知W随着a的增大而增大从而求解。
【考点精析】关于本题考查的一次函数的性质,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
 ,且满足式子
,且满足式子 .
.(1)求出
 的值;
的值;(2)①在
 轴的正半轴上存在一点
轴的正半轴上存在一点 ,使
,使 的面积等于
的面积等于 的面积的一半,求出点
的面积的一半,求出点 的坐标;
的坐标; ②在坐标轴的其它位置是否存在点
 ,使
,使 的面积等于
的面积等于 的面积的一半仍然成立,若存在,直接写出其他符合条件的点
的面积的一半仍然成立,若存在,直接写出其他符合条件的点 的坐标;
的坐标;(3)如图2,过点
 作
作 轴交
轴交 轴于点
轴于点 ,点
,点 为线段
为线段 延长线上一动点,连接
延长线上一动点,连接 ,
, 平分
平分 ,
, ,当点
,当点 运动时,求证:
运动时,求证:

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲
乙
价格(万元/台)
7
5
每台日产量(个)
100
60
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,CF平分∠ECD,HC⊥CF交直线AB于H,AG平分∠HAE交HC于G,EJ∥AG交CF于J,∠AEC=80°,则下列结论正确的有( )个.
①∠BAE+∠ECD=80°;②CG平分∠ICE;③∠AGC=140°;④∠EJC﹣∠AGH=90°.

A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=115°,∠ACF=25°,则∠FEC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边
是等边 的边
的边 上一点,
上一点, 是
是 延长线上一点,
延长线上一点, 连
连 接交
接交 于
于 ,过
,过 点作
点作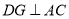 于
于 点.证明下列结论:
点.证明下列结论:

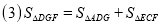

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD的各边分别平行于x轴或y轴,A,B,C,D的坐标分别为(﹣2,1)(2,1)(2,﹣1)(﹣2,﹣1)物体甲和物体乙分别由E(﹣2,0)和F(2,0)同时出发,沿长方形的边按逆时针方向同向行进,甲的速度每秒4个单位长度,乙的速度每秒1个单位长度,则两个物体第2019次相遇地点的坐标为_____.

相关试题

