【题目】如图,AB∥CD,CF平分∠ECD,HC⊥CF交直线AB于H,AG平分∠HAE交HC于G,EJ∥AG交CF于J,∠AEC=80°,则下列结论正确的有( )个.
①∠BAE+∠ECD=80°;②CG平分∠ICE;③∠AGC=140°;④∠EJC﹣∠AGH=90°.

A.1B.2C.3D.4
参考答案:
【答案】D
【解析】
作ET∥BH,如图1,由平行公理的推论可得ET∥CD,然后利用平行线的性质和角的和差即可判断①;
由垂直的定义可得∠ECH+∠ECF=90°,然后根据平角的定义和角平分线的定义即可判断②;
同①的方法可得∠AGC=∠GAH+∠GCI,然后根据角平分线的定义和①的结论即可判断③;
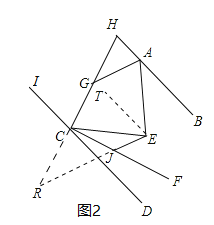
延长HC交EJ的延长线于R,如图2,由平行线的性质可得∠AGH=∠R,然后根据三角形的外角性质和已知条件HC⊥CF即可判断④.
解:作ET∥BH,如图1,则∠BAE=∠AET,
∵DC∥BH,
∴ET∥CD,
∴∠ECD=∠CET,
∴∠AEC=∠AET+∠CET=∠BAE+∠ECD=80°,故①正确;
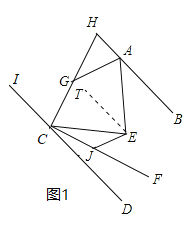
∵HC⊥CF,
∴∠ECH+∠ECF=90°,∠FCD+∠HCI=90°,
∵∠ECF=∠FCD,
∴∠ECH=∠HCI,
∴CH平分∠ECI,故②正确;
同①的方法可证:∠AGC=∠GAH+∠GCI=![]() (∠EAH+∠ECI)=
(∠EAH+∠ECI)=![]() (360°﹣∠BAE﹣∠ECD)=
(360°﹣∠BAE﹣∠ECD)=![]() (360°﹣80°)=140°,故③正确;
(360°﹣80°)=140°,故③正确;
延长HC交EJ的延长线于R,如图2,
∵AG∥ER,
∴∠AGH=∠R,
∵∠EJC=∠R+∠RCJ,∠RCJ=90°,
∴∠EJC﹣∠AGH=90°,故④正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 是直角,
是直角, 平分
平分 平分
平分
 当
当 ,求
,求 的度数.
的度数.(2)若
 ,求
,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
 ,且满足式子
,且满足式子 .
.(1)求出
 的值;
的值;(2)①在
 轴的正半轴上存在一点
轴的正半轴上存在一点 ,使
,使 的面积等于
的面积等于 的面积的一半,求出点
的面积的一半,求出点 的坐标;
的坐标; ②在坐标轴的其它位置是否存在点
 ,使
,使 的面积等于
的面积等于 的面积的一半仍然成立,若存在,直接写出其他符合条件的点
的面积的一半仍然成立,若存在,直接写出其他符合条件的点 的坐标;
的坐标;(3)如图2,过点
 作
作 轴交
轴交 轴于点
轴于点 ,点
,点 为线段
为线段 延长线上一动点,连接
延长线上一动点,连接 ,
, 平分
平分 ,
, ,当点
,当点 运动时,求证:
运动时,求证:

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲
乙
价格(万元/台)
7
5
每台日产量(个)
100
60
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司承接A,B两种货物运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨;该物流公司6月承接的A种货物和B种数量与5月份相同,6月份共收取运费13000元.
(1)该物流公司月运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收到多少运输费? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=115°,∠ACF=25°,则∠FEC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边
是等边 的边
的边 上一点,
上一点, 是
是 延长线上一点,
延长线上一点, 连
连 接交
接交 于
于 ,过
,过 点作
点作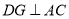 于
于 点.证明下列结论:
点.证明下列结论:


相关试题

