【题目】超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)

参考答案:
【答案】没有超速.
【解析】试题分析:直接构造直角三角形,再利用特殊角的三角函数关系得出AB的长,进而求出汽车的速度,进而得出答案.
试题解析:解:这辆汽车没有超速,理由:过点D作DF⊥CB于点F,过点D作DE⊥AC于点E,由题意可得:∠ACD=30°,∠DCB=45°,∠CDB=75°,则∠DAE=45°,∠CDF=45°,∠FDB=30°,设BF=x,则DF=CF=![]() x,∵BC=200m,∴
x,∵BC=200m,∴![]() x+x=200,解得:x=100(
x+x=200,解得:x=100(![]() ﹣1),故BF=100(
﹣1),故BF=100(![]() ﹣1)m,则BD=200(
﹣1)m,则BD=200(![]() ﹣1)m,DC=
﹣1)m,DC=![]() DF=
DF=![]() ×
×![]() ×100(
×100(![]() ﹣1)=(300
﹣1)=(300![]() ﹣100
﹣100![]() )m,故DE=(150
)m,故DE=(150![]() ﹣50
﹣50![]() )m,则AD=
)m,则AD=![]() (150
(150![]() ﹣50
﹣50![]() )=(300﹣100
)=(300﹣100![]() )m,故AB=AD+BD=300﹣100
)m,故AB=AD+BD=300﹣100![]() +200(
+200(![]() ﹣1)=100(
﹣1)=100(![]() +1)≈173(m),∴
+1)≈173(m),∴![]() ≈24.7(m/s),∵每小时120千米=
≈24.7(m/s),∵每小时120千米=![]() ≈33.3(m/s),∵24.7<33.3,∴这辆车没有超速.
≈33.3(m/s),∵24.7<33.3,∴这辆车没有超速.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:

如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________ _________),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________ ________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).
-
科目: 来源: 题型:
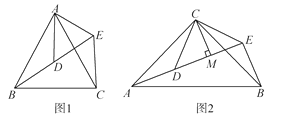
查看答案和解析>>【题目】(1)如图1,△ABC与△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①求∠AEB的度数;
②证明:AE=BE+2CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,CE,BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3……
第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为En.

(1)如图①,求证:∠E=∠B+∠C;
(2)如图②,求证:∠E1=
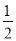 ∠E;
∠E;(3)猜想:若∠En=b°,求∠BEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解七年级学生的学习情况,在这个年级抽取了50名学生对某课进行了测试。将所得的成绩(成绩均为整数)进行整理(如下边所示),请你画出频数分布直方图和频数折线图,并回答问题:
分数
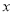





频率
0.04
0.04
0.16
0.34
0.42
 这次测试及格(包括60分)的人数有多少?
这次测试及格(包括60分)的人数有多少?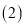 本次测试这50名学生成绩的优秀率是多少?(90分以上为优秀,包括90分)
本次测试这50名学生成绩的优秀率是多少?(90分以上为优秀,包括90分) 这个年级此学科学习情况如何?
这个年级此学科学习情况如何? -
科目: 来源: 题型:
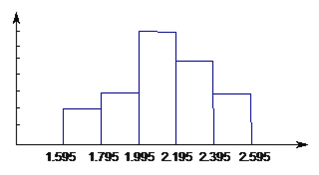
查看答案和解析>>【题目】某校七年级学生进行体育测试,七年级(2)班男生的立定跳远成绩制成频数分布直方图,图中从左到右各矩形的高之比是
 ,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。
,最后一组的频数是6,根据直方图所表达的信息,解答下列问题。(1)该班有多少名男生?
(2)若立定跳远的成绩在2.0米以上(包括2.0米)为合格率是多少
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会准备调查全校七年级学生 每天(除课间操外)的课外锻炼时间。
(1)确定调查方式时,甲说:“我到(1)班去调查全体同学”;乙同学说:“我到体育场上去询问参加锻炼的同学”;丙同学说:“我到全校七年级每个班去随机调查一定数量的同学”。你认为调查方式最合理的是(填“甲”、或“乙”或“丙”)_________
(2)他们采用了最为合适的调查方法收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请将两幅统计图补充完整;


(3)若该七年级共有1200名同学,请你估计其中每天(除课间操外)课外锻炼时间不大于20分钟的人数。
相关试题

