【题目】如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )

A. 30 B. 34 C. 36 D. 40
参考答案:
【答案】B
【解析】在Rt△AEH中,由勾股定理求出EH=![]() ,根据正方形面积公式求出即可
,根据正方形面积公式求出即可
解: ∵四边形ABCD是正方形, AE=BF=CG=DH, ∴AH=DG=CF=BE,
∴△AEH≌△DHG≌△CGF≌△BFE(SAS),
∴EH=EF=FG=HG,∵∠A=∠D=90°,
∴∠DGH+∠DHG=90°,
∴∠AHE+∠DHG=90°,
∴∠EHG=180°-90°=90°,
∴四边形EFGH是正方形,
在Rt△AEH中,AE=2,AH=5,由勾股定理得:EH=![]() =
=![]() ,
,
∵四边形EFGH是正方形,
∴EF=FG=GH=EH=![]() ,
,
∴四边形EFGH的面积是(![]() )2=34.
)2=34.
故选B.
“点睛”本题考查了正方形性质,全等三角形的性质和判定,三角形内角和定理,正方形判定的应用,关键是推出四边形EFGH是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )

A.2cm2 B.4cm2 C.6cm2 D.8cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,有A、B两动点在线段MN上各自做不间断往返匀速运动(即只要动点与线段MN的某一端点重合则立即转身以同样的速度向MN的另一端点运动,与端点重合之前动点运动方向、速度均不改变),已知A的速度为3米/秒,B的速度为2米/秒
(1)已知MN=100米,若B先从点M出发,当MB=5米时A从点M出发,A出发后经过 秒与B第一次重合;
(2)已知MN=100米,若A、B同时从点M出发,经过 秒A与B第一次重合;
(3)如图2,若A、B同时从点M出发,A与B第一次重合于点E,第二次重合于点F,且EF=20米,设MN=s米,列方程求s.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各图中的MA1与NAn平行.

(1)图①中的∠A1+∠A2= 度,图②中的∠A1+∠A2+∠A3= 度,
图③中的∠A1+∠A2+∠A3+∠A4= 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度,…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10= 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:
①△ABD和△ACD面积相等;
②∠BAD=∠CAD;
③△BDF≌△CDE;
④BF∥CE;
⑤CE=AE.
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
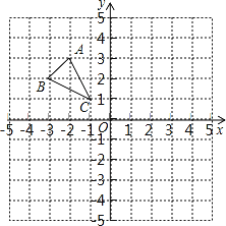
查看答案和解析>>【题目】如图,△ABC的顶点分别为A(-2,3),B(-3,2),C(-1,1)
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)请在x轴上确定一点D,使点D到B、C的距离相等(要求用直尺和圆规作图,并保留作图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
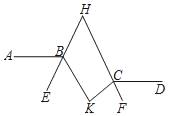
A. 76° B. 78° C. 80° D. 82°
相关试题

