【题目】如图,抛物线y=ax2+bx+c与x轴相交于点A、B(m+2,0)与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是 . 
参考答案:
【答案】(﹣2,0)
【解析】解:由C(0,c),D(m,c),得函数图象的对称轴是x= ![]() , 设A点坐标为(x,0),由A、B关于对称轴x=
, 设A点坐标为(x,0),由A、B关于对称轴x= ![]() ,得
,得![]() =
= ![]() ,
,
解得x=﹣2,
即A点坐标为(﹣2,0),
所以答案是:(﹣2,0).
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是( )
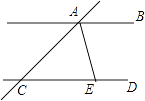
A.40°
B.70°
C.80°
D.140° -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程2x2+x﹣a=0有两个不相等的实数根,则实数a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(
 +1)(
+1)(  ﹣1)+(﹣2)0﹣
﹣1)+(﹣2)0﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组
家庭用水量x/吨
家庭数/户
A
0≤x≤4.0
4
B
4.0<x≤6.5
13
C
6.5<x≤9.0
D
9.0<x≤11.5
E
11.5<x≤14.0
6
F
x>4.0
3
根据以上信息,解答下列问题

(1)家庭用水量在4.0<x≤6.5范围内的家庭有户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是%;
(2)本次调查的家庭数为户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是%;
(3)家庭用水量的中位数落在组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2﹣3x+
 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E 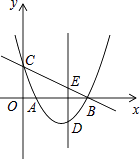
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.
相关试题

