【题目】基本模型:如图1,点A,F,B在同一直线上,若∠A=∠B=∠EFC=90°,易得△AFE~△BCF. 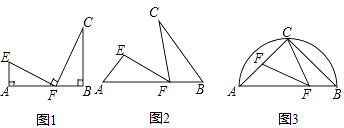
(1)模型拓展:如图2,点A,F,B在同一直线上,若∠A=∠B=∠EFC,求证:△AFE~△BCF;
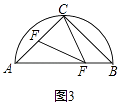
(2)拓展应用:如图3,AB是半圆⊙O的直径,弦长AC=BC=4 ![]() ,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
参考答案:
【答案】
(1)证明:如图2,∵∠A=∠EFC,
∴∠E+∠EFA=∠EFA+∠CFB,
∴∠E=∠CFB,
∵∠A=∠B,
∴△AFE∽△BCF
(2)解:如图3,∵AB是⊙O的直径,
∴∠ACB=90°,
∴AB= ![]() =8,
=8,
∵AC=BC,
∴∠A=∠B=45°,
∴∠A=∠B=∠CFE=45°,
由(1)可得△AFE∽△BCF,
∴ ![]() ,
,
即 ![]() ,
,
∴y=﹣ ![]() x2+
x2+ ![]() x(0≤x≤8),
x(0≤x≤8),
【解析】(1)利用已知得出∠E=∠CFB,进而利用相似三角形的判定方法得出即可;(2)利用(1)得出△AFE∽△BCF,则 ![]() ,进而求出y与x的函数关系式.
,进而求出y与x的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个可以自由转动的均匀转盘A、B,都被分成了3等份,并在每份内均标有数字,如图所示,规则如下:
①分别转动转盘A、B.
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).
(1)用列表法(或树状图)分别求出数字之积为3的倍数和为5的倍数的概率;
(2)小亮和小芸想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得2分;数字之积为5的倍数时,小芸得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏双方公平. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品公司为指导某种应季商品的生产和销售,在对历年市场行情和生产情况进行调查基础上,对今年这种商品的市场售价和生产成本进行了预测并提供了两个方面的信息:如图(1)(2).
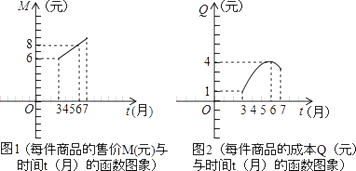
注:两图中的每个实心黑点所对应的纵坐标分别指相应月份一件商品的售价和成本,生产成本6月份最高;图(1)的图象是线段,图(2)的图象是抛物线.
(1)在3月份出售这种商品,一件商品的利润是多少?
(2)设t月份出售这种商品,一件商品的成本Q(元),求Q关于t的函数解析式.
(3)设t月份出售这种商品,一件商品的利润W(元),求W关于t的函数解析式.
(4)问哪个月出售这种商品,一件商品的利润最大?简单说明理由. -
科目: 来源: 题型:
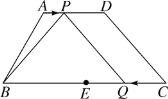
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=60°,AB=8,BC=16,AD=6.E是BC的中点,点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动,设运动时间为t秒.
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t=________时,△BPQ的面积与四边形PQCD的面积相等;
(3)当t为何值时,以点P,Q,E,D为顶点的四边形是平行四边形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动,已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG,设E点移动距离为x(x>0).
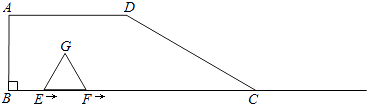
(1)△EFG的边长是(用含有x的代数式表示),当x=2时,点G的位置在;
(2)若△EFG与梯形ABCD重叠部分面积是y,求y与x之间的函数关系式;
(3)探究(2)中得到的函数y在x取何值时,存在最大值?并求出最大值. -
科目: 来源: 题型:
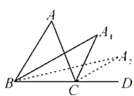
查看答案和解析>>【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2…∠A2 017BC和∠A2 017CD的平分线交于点A2 018,则∠A2 018=_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列填空:
已知:如图,AB∥CD,∠B=120°,CA平分∠BCD.求证:∠1=30°.
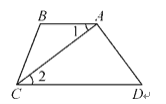
证明:∵AB∥CD( ),
∴∠B+∠BCD= ( ).
∵∠B= ( ),
∴∠BCD= ( ).
又∵CA平分∠BCD( ),
∴∠2= ( ).
∵AB∥CD( ),
∴∠1= =30°( ).
相关试题

