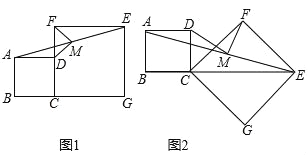
【题目】已知正方形ABCD和正方形CGEF,且D点在CF边上,M为AE中点,连接MD、MF,
(1)如图1,请直接给出线段MD、MF的数量及位置关系是 ;
(2)如图2,把正方形CGEF绕点C顺时针旋转,则(1)中的结论是否成立?若成立,请证明;若不成立,请给出你的结论并证明;
(3)若将正方形CGEF绕点C顺时针旋转30°时,CF边恰好平分线段AE,请直接写出![]() 的值.
的值.
参考答案:
【答案】(1)MD=MF,MD⊥MF;(2)MD=MF,MD⊥MF仍成立,理由详见解析;(3)![]() .
.
【解析】
试题分析:(1)延长DM交EF于点P,易证AM=EM,即可证明△ADM≌△EPM,可得DM=PM,根据△DFP是直角三角形即可解题;
(2)延长DM交CE于点N,连接FN、DF,易证∠DAM=∠NEM,即可证明△ADM≌△ENM,可得EN=AD,DM=MN,可证CD=EN,即可证明△CDF≌△ENF,可得DF=NF,即可解题;
(3)根据(1)可得MD=MF,MD⊥MF,若CF边恰好平分线段AE,则CF过点M,最后根据Rt△CDM中,∠DCF=30°,即可求得![]() 的值.
的值.
试题解析:(1)线段MD、MF的数量及位置关系是MD=MF,MD⊥MF,
理由:如图1,延长DM交EF于点P,
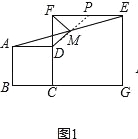
∵四边形ABCD和四边形FCGE是正方形,
∴AD∥EF,∠MAD=∠MEP,∠CFE=90°.
∴△DFP是直角三角形.
∵M为AE的中点,
∴AM=EM.
在△ADM和△EPM中,
∠MAD=∠MEP,AM=EM,∠AMD=∠EMP,
∴△ADM≌△EPM(ASA),
∴DM=PM,AD=PE,
∴M是DP的中点.
∴MF=![]() DP=MD,
DP=MD,
∵AD=CD,
∴CD=PE,
∵FC=FE,
∴FD=FP,
∴△DFP是等腰直角三角形,
∴FM⊥DP,即FM⊥DM.
故答案为:MD=MF,MD⊥MF;
(2)MD=MF,MD⊥MF仍成立.
证明:如图2,延长DM交CE于点N,连接FN、DF,
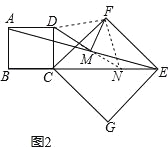
∵CE是正方形CFEG对角线,
∴∠FCN=∠CEF=45°,
∵∠DCE=90°,
∴∠DCF=45°,
∵AD∥BC,
∴∠DAM=∠NEM,
在△ADM和△ENM中,∠MAD=∠NEM,AM=EM,∠AMD=∠EMN,
∴△ADM≌△ENM(ASA),
∴EN=AD,DM=MN,
∵AD=CD,
∴CD=EN,
在△CDF和△ENF中,
CD=EN,∠DCF=∠CEF=45°,CF=EF,
∴△CDF≌△ENF,(SAS)
∴DF=NF,
∴FM=DM,FM⊥DM.
(3)如图所示,若CF边恰好平分线段AE,则CF过点M,
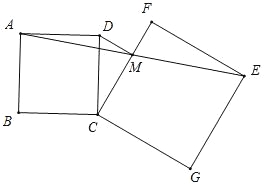
由(1)可得FM=DM,FM⊥DM,
设FM=DM=1,
∵∠DCF=30°,
∴Rt△DCM中,CM=![]() ,CD=2=CB,
,CD=2=CB,
∴CF=![]() +1=CG,
+1=CG,
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线y=2x+t﹣3与函数y=
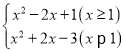 的图象有且只有两个公共点时,则t的取值范围是 .
的图象有且只有两个公共点时,则t的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列说法:①过两点有且只有一条直线;②两点之间,线段最短;③若AB=BC,则点B是线段AC的中点;④射线AB和射线BA是同一条射线;⑤平角是一条直线.其中正确的个数是( )
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】画一根数轴,用数轴上的点把如下的有理数﹣2,﹣0.5,0,﹣4表示出来,并用“<”把它们连接起来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(2a﹣1)2+|2a+b|=0,且|c﹣1|=2,求c(a3﹣b)的值.
-
科目: 来源: 题型:
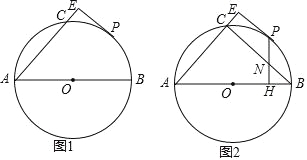
查看答案和解析>>【题目】如图1,AB是⊙O的直径,AC是弦,点P是
 的中点,PE⊥AC交AC的延长线于E.
的中点,PE⊥AC交AC的延长线于E.(1)求证:PE是⊙O的切线;
(2)如图2,作PH⊥AB于H,交BC于N,若NH=3,BH=4,求PE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)

(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
相关试题

