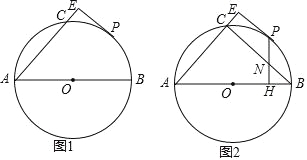
【题目】如图1,AB是⊙O的直径,AC是弦,点P是![]() 的中点,PE⊥AC交AC的延长线于E.
的中点,PE⊥AC交AC的延长线于E.
(1)求证:PE是⊙O的切线;
(2)如图2,作PH⊥AB于H,交BC于N,若NH=3,BH=4,求PE的长.
参考答案:
【答案】(1)证明详见解析;(2)8.
【解析】
试题分析:(1)连接BC、OP,由AB是⊙O的直径、PE⊥AE知PE∥BC,根据点P是![]() 的中点知OP⊥BC,即可得OP⊥PE,得证;
的中点知OP⊥BC,即可得OP⊥PE,得证;
(2)由(1)知,四边形PECQ是矩形,从而可设PE=CQ=BQ=x,根据勾股定理求得BN的长,先证△BHN∽△BQO得![]() ,表示出BO、OQ的长,再证△PQN∽△BHN得
,表示出BO、OQ的长,再证△PQN∽△BHN得![]() ,即
,即 ,求出x即可.
,求出x即可.
试题解析:(1)如图1,连接BC、OP,
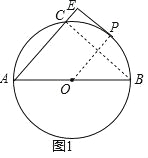
∵AB是⊙O的直径,
∴∠ACB=90°,即BC⊥AE,
又∵PE⊥AE,
∴PE∥BC,
∵点P是![]() 的中点,
的中点,
∴OP⊥BC,
∴OP⊥PE,
∴PE是⊙O的切线;
(2)如图2,连接OP,
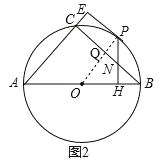
由(1)知,四边形PECQ是矩形,
∴设PE=CQ=BQ=x,
∵NH=3,BH=4,PH⊥AB,
∴BN=5,
∵∠B=∠B,∠BHN=∠BQO=90°,
∴△BHN∽△BQO,
∴![]() ,即
,即![]() ,
,
解得:BO=![]() ,OQ=
,OQ=![]() ,
,
∴PQ=PO﹣OQ=BO﹣OQ=![]() ,
,
∵∠PNQ=∠BNH,∠PQN=∠BHN=90°,
∴△PQN∽△BHN,
∴![]() ,即
,即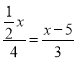 ,
,
解得:x=8,
∴PE=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】画一根数轴,用数轴上的点把如下的有理数﹣2,﹣0.5,0,﹣4表示出来,并用“<”把它们连接起来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD和正方形CGEF,且D点在CF边上,M为AE中点,连接MD、MF,
(1)如图1,请直接给出线段MD、MF的数量及位置关系是 ;
(2)如图2,把正方形CGEF绕点C顺时针旋转,则(1)中的结论是否成立?若成立,请证明;若不成立,请给出你的结论并证明;
(3)若将正方形CGEF绕点C顺时针旋转30°时,CF边恰好平分线段AE,请直接写出
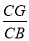 的值.
的值.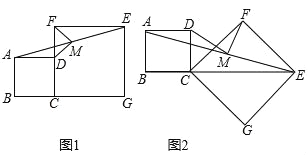
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(2a﹣1)2+|2a+b|=0,且|c﹣1|=2,求c(a3﹣b)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)

(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面内有三点,经过每两点作一条直线,则能作出的直线的条数是 ( )
A. 1条 B. 3条 C. 1条或3条 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,全班男同学进行了100米测验,达标成绩为15秒,下表是某小组8名男生的成绩测试记录,其中“+”表示成绩大于15秒.问:
﹣0.8
+1
﹣1.2
0
﹣0.7
+0.6
﹣0.4
﹣0.1
(1)这个小组男生的达标率为多少?(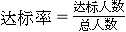 )
)
(2)这个小组男生的平均成绩是多少秒?
相关试题

