【题目】在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y1 | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
y2 | … | 0 | 2 | 4 | 6 | 8 | 10 | 12 | … |
请你根据表格信息回答下列问题,
(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为 ;
(2)当y1>y2时,自变量x的取值范围是 ;
(3)请写出二次函数y1=ax2+bx+c的三条不同的性质.
参考答案:
【答案】(1)(0,﹣3);(2)当x<﹣1或x>5时,二次函数的值大于一次函数的值.(3)见解析
【解析】
试题分析:(1)令x=0,求得y的数值,确定与y轴交点坐标即可;
(2)先利用待定系数法求出二次函数与一次函数的解析式,求出两函数图象的交点,进而可得出结论;
(3)利用二次函数的性质:开口方向,对称轴,增减性直接得出答案即可.
解:(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为(0,﹣3);
(2)由题意得,
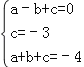 ,
,
解得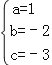 .
.
∴二次函数的解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4.
∵一次函数y2=kx+m的图象过点(﹣1,0),(0,2),
∴![]() ,
,
解得![]() .
.
∴一次函数的解析式为y=2x+2,
如图所示,
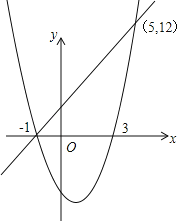
当x<﹣1或x>5时,二次函数的值大于一次函数的值.
(3)该函数的图象开口向上;当x=1时,函数有最大值;当x<1时,y随x的增大而减小,当x≥1时,y随x的增大而增大;顶点坐标为(1,﹣4);对称轴为直线x=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:3x2﹣6x+3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左到右的变形正确的是( )
A.﹣2x+4y=﹣2(x﹣4y)
B.a2﹣6=(a+2)(a﹣3)
C.(a+b)2=a2+b2
D.x2﹣y2=(x﹣y)(x+y) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,A(0,4),C(3,0).
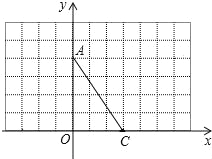
(1)①画出线段AC关于y轴对称线段AB;
②将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD;
(2)若直线y=kx平分(1)中四边形ABCD的面积,请直接写出实数k的值.
-
科目: 来源: 题型:
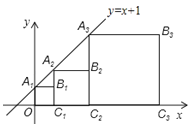
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B6的坐标是
-
科目: 来源: 题型:
查看答案和解析>>【题目】宜兴紧靠太湖,所产百合有“太湖人参”之美誉,今年百合上市后,甲、乙两超市分别用12000元以相同的进价购进质量相同的百合,甲超市销售方案是:将百合按分类包装销售,其中挑出优质的百合400千克,以进价的2倍价格销售,剩下的百合以高于进价10%销售.乙超市的销售方案是:不将百合分类,直接包装销售,价格按甲超市分类销售的两种百合售价的平均数定价.若两超市将百合全部售完,其中甲超市获利8400元(其它成本不计).问:
(1)百合进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.

(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是: ;
(3)画出AB边上的高线CD;
(4)画出△ABC中AB边上的中线CE;
(5)△BCE的面积为 .
相关试题

