【题目】宜兴紧靠太湖,所产百合有“太湖人参”之美誉,今年百合上市后,甲、乙两超市分别用12000元以相同的进价购进质量相同的百合,甲超市销售方案是:将百合按分类包装销售,其中挑出优质的百合400千克,以进价的2倍价格销售,剩下的百合以高于进价10%销售.乙超市的销售方案是:不将百合分类,直接包装销售,价格按甲超市分类销售的两种百合售价的平均数定价.若两超市将百合全部售完,其中甲超市获利8400元(其它成本不计).问:
(1)百合进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
参考答案:
【答案】(1)百合进价为每千克20元;(2)8400元,两种销售方式获利一样多.
【解析】
试题分析:(1)设百合进价为每千克x元,根据甲超市获利8400元列出分式方程,求出方程(2)根据(1)求出甲乙两超市购进百合得质量数,求出甲超市分类销售的两种百合售价的平均数定价,即为乙超市的定价,进而求出乙超市的利润,即可做出判断.
试题解析:(1)设百合进价为每千克x元,
根据题意得:400×(2x-x)+(![]() -400)×10%x=8400,
-400)×10%x=8400,
解得:x=20,
经检验x=20是分式方程的解,且符合题意,
则百合进价为每千克20元;
(2)甲乙两超市购进百合的质量数为![]() =600(千克),
=600(千克),
根据(1)得:甲超市平均定价为2×20×![]() +20×(1+10%)×
+20×(1+10%)×![]() =34(元/千克),即乙超市售价为34元/千克,
=34(元/千克),即乙超市售价为34元/千克,
乙超市获利为600×(34-20)=8400(元),则两种销售方式获利一样多.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,A(0,4),C(3,0).
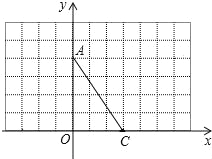
(1)①画出线段AC关于y轴对称线段AB;
②将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD;
(2)若直线y=kx平分(1)中四边形ABCD的面积,请直接写出实数k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:
x
…
﹣1
0
1
2
3
4
5
…
y1
…
0
﹣3
﹣4
﹣3
0
5
12
…
y2
…
0
2
4
6
8
10
12
…
请你根据表格信息回答下列问题,
(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为 ;
(2)当y1>y2时,自变量x的取值范围是 ;
(3)请写出二次函数y1=ax2+bx+c的三条不同的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B6的坐标是
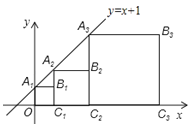
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.

(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是: ;
(3)画出AB边上的高线CD;
(4)画出△ABC中AB边上的中线CE;
(5)△BCE的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算2015×2015-2015×2014-2014×2013+2014×2014的值是( )
A. 1 B. -1 C. 4029 D. 4030
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年某县有1万名初中和小学生参加全国义务教育质量抽测,为了了解1万名学生的抽测成绩,从中抽取500名学生抽测成绩进行统计分析,在这个问题中数据500是( )
A.总体
B.个体
C.一个样本
D.样本容量
相关试题

