【题目】将一列有理数-1,2,-3,4,-5,6,…如图排序,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么“峰4”中C的位置是有理数________,有理数“2018”应排在A,B,C,D,E中的________位置.

参考答案:
【答案】 -19 B
【解析】观察不难发现,每个峰排列5个数,求出5个峰排列的数的个数,再求出,“峰4”中C位置的数的序数,然后根据排列的奇数为负数,偶数为正数解答;用(2018-1)除以5,根据商和余数的情况确定所在峰中的位置即可.
∵每个峰需要5个数,
∴5×3=15,
15+1+3=19,
∴“峰4”中C位置的数的是-19,
∵(2018-1)÷5=403…2,
∴2008为“峰403”的第二个数,排在B的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式成立的是( )
A. (-a-b)2+(a-b)2=-4ab B. (-a-b)2+(a-b)2=a2+b2
C. (-a-b)(a-b)=(a-b)2 D. (-a-b)(a-b)=b2-a2
【答案】D
【解析】解析:∵(-a-b)2+(a-b)2=(a+b)2+(a-b)2=(a2+2ab+b2)+(a2-2ab+b2)=2a2+2b2,
∴选项A与选项B错误;
∵(-a-b)(a-b)=-(a+b)(a-b)=-(a2-b2)=b2-a2,∴选项C错误,选项D正确.
故选D.
【题型】单选题
【结束】
8【题目】若x=1,y=
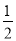 ,则x2+4xy+4y2的值是( )
,则x2+4xy+4y2的值是( )A. 2 B. 4 C. 32 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=1,y=
 ,则x2+4xy+4y2的值是( )
,则x2+4xy+4y2的值是( )A. 2 B. 4 C. 32 D. 12
【答案】B
【解析】解析:x2+4xy+4y2=(x+2y)2=
 =4.故选B.
=4.故选B.【题型】单选题
【结束】
9【题目】下列因式分解,正确的是( )
A. x2y2-z2=x2(y+z)(y-z) B. -x2y+4xy-5y=-y(x2+4x+5)
C. (x+2)2-9=(x+5)(x-1) D. 9-12a+4a2=-(3-2a)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
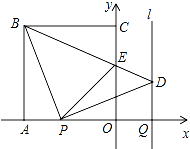
(1)∠PBD的度数为 , 点D的坐标为(用t表示);
(2)当t为何值时,△PBE为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
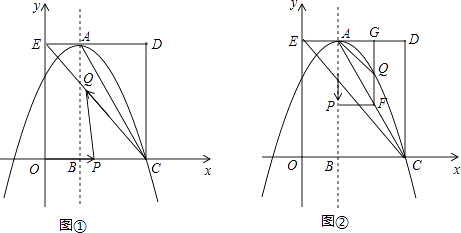
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上点A表示数x,点B表示-2,点C表示数2x+8.
(1)若将数轴沿点B对折,点A与点C恰好重合,则点A和点C分别表示什么数?
(2)若BC=4AB,则点A和点C分别表示什么数?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解,正确的是( )
A. x2y2-z2=x2(y+z)(y-z) B. -x2y+4xy-5y=-y(x2+4x+5)
C. (x+2)2-9=(x+5)(x-1) D. 9-12a+4a2=-(3-2a)2
【答案】C
【解析】解析:选项A.用平方差公式法,应为x2y2-z2=(xy+z)·(xy-z),故本选项错误.
选项B.用提公因式法,应为-x2y+ 4xy-5y=- y(x2- 4x+5),故本选项错误.
选项C.用平方差公式法,(x+2)2-9=(x+2+3)(x+2-3)=(x+5)(x-1),故本选项正确.
选项D.用完全平方公式法,应为9-12a+4a2=(3-2a)2,故本选项错误.
故选C.
点睛:(1)完全平方公式:
 .
.(2)平方差公式:(a+b)(a-b)=
 .
.(3)常用等价变形:

 ,
, ,
,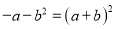 .
.【题型】单选题
【结束】
10【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
相关试题

