【题目】已知二次函数的图象经过A(2,0)、C(0,12)两点,且对称轴为直线x=4.设顶点为点P,与x轴的另一交点为点B.
(1)求二次函数的解析式及顶点P的坐标;
(2)如图1,在直线 y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;
(3)如图2,点M是线段OP上的一个动点(O、P两点除外),以每秒 ![]() 个单位长度的速度由点P向点O 运动,过点M作直线MN∥x轴,交PB于点N.将△PMN沿直线MN对折,得到△P1MN.在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒.求S关于t的函数关系式.
个单位长度的速度由点P向点O 运动,过点M作直线MN∥x轴,交PB于点N.将△PMN沿直线MN对折,得到△P1MN.在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒.求S关于t的函数关系式.
参考答案:
【答案】
(1)
解:设二次函数的解析式为y=ax2+bx+c
由题意得  ,
,
解得  ,
,
∴二次函数的解析式为y=x2﹣8x+12,
点P的坐标为(4,﹣4)
(2)
解:方法一:
存在点D,使四边形OPBD为等腰梯形.理由如下:
当y=0时,x2﹣8x+12=0,
∴x1=2,x2=6,
∴点B的坐标为(6,0),
设直线BP的解析式为y=kx+m
则 ![]() ,
,
解得 ![]()
∴直线BP的解析式为y=2x﹣12
∴直线OD∥BP,
∵顶点坐标P(4,﹣4),
∴OP=4 ![]()
设D(x,2x)则BD2=(2x)2+(6﹣x)2
当BD=OP时,(2x)2+(6﹣x)2=32,
解得:x1= ![]() ,x2=2,
,x2=2,
当x2=2时,OD=BP= ![]() ,四边形OPBD为平行四边形,舍去,
,四边形OPBD为平行四边形,舍去,
∴当x= ![]() 时四边形OPBD为等腰梯形,
时四边形OPBD为等腰梯形,
∴当D( ![]() ,
, ![]() )时,四边形OPBD为等腰梯形
)时,四边形OPBD为等腰梯形
方法二:
设D(t,2t),O(0,0),P(4,﹣4),B(6,0),
∴KBP= ![]() =2,KOD=
=2,KOD= ![]() =2,
=2,
∴KBP=KOD,
∴BP∥OD,
∵四边形OPBD为等腰梯形,∴DB=OP,
(t﹣6)2+(2t﹣0)2=(4﹣0)2+(﹣4﹣0)2,
∴t1=2(舍),t2= ![]() ,∴D(
,∴D( ![]() ,
, ![]() )
)

(3)
解:方法一:
①当0<t≤2时,
∵运动速度为每秒 ![]() 个单位长度,运动时间为t秒,则MP=
个单位长度,运动时间为t秒,则MP= ![]() t,
t,
∴PH=t,MH=t,HN= ![]() (4﹣t),
(4﹣t),
∴MN=MH+HN=2+ ![]() t,
t,
∴S= ![]() t2;
t2;
②当2<t<4时,P1G=2t﹣4,P1H=t,
∵MN∥OB
∴△P1EF∽△P1MN,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() =3t2﹣12t+12,
=3t2﹣12t+12,
∴S= ![]() t2﹣(3t2﹣12t+12)=﹣
t2﹣(3t2﹣12t+12)=﹣ ![]() t2+12t﹣12,
t2+12t﹣12,
∴当0<t≤2时,S= ![]() t2,
t2,
当2<t<4时,S=﹣ ![]() t2+12t﹣12
t2+12t﹣12
方法二:
O(0,0),P(4,﹣4),
∴lOP:y=﹣x,
∴M(4﹣t,t﹣4),
∵B(6,0),∴lBP:y=2x﹣12,
∴N( ![]() ,t﹣4),
,t﹣4),
①当0<t≤2时,S= ![]() =
= ![]() =
= ![]() ,
,
②当2<t<4时,
∵△PMN与△P′MN关于MN对称,
∴KMP′+KMP=0,KNP′+KNP=0,
∴lMP′:y=x+2t﹣8,lNP′:y=﹣2x+2t+4,
∴D(8﹣2t,0),C(t+2,0),
∴S= ![]() (CD+MN)|MY|=
(CD+MN)|MY|= ![]() =﹣
=﹣ ![]() .
.


【解析】(1)利用对称轴公式,A、C两点坐标,列方程组求a、b、c的值即可;(2)存在.由(1)可求直线PB解析式为y=2x﹣12,可知PB∥OD,利用BD=PO,列方程求解,注意排除平行四边形的情形;(3)由P(4,﹣4)可知直线OP解析式为y=﹣x,当P1落在x轴上时,M、N的纵坐标为﹣2,此时t=2,按照0<t≤2,2<t<4两种情形,分别表示重合部分面积.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长春外国语学校为了创建全省“最美书屋”,购买了一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多5元.已知学校用12000元购买的科普类图书的本数与用9000元购买的文学类图书的本数相等,求学校购买的科普类图书和文学类图书平均每本的价格各是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人从
 ,
,  两地同时出发,甲骑自行车,乙骑摩托车,沿同一条直线公路相向匀速行驶.出发后经
两地同时出发,甲骑自行车,乙骑摩托车,沿同一条直线公路相向匀速行驶.出发后经 小时两人相遇.已知在相遇时乙比甲多行驶了
小时两人相遇.已知在相遇时乙比甲多行驶了 千米,且摩托车的速度是自行车速度的
千米,且摩托车的速度是自行车速度的 倍.
倍.(1)问甲、乙行驶的速度分别是多少?
(2)甲、乙行驶多少小时,两车相距
 千米?
千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点P与点C不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接AA1 , 射线AA1分别交射线PB、射线B1B于点E、F.
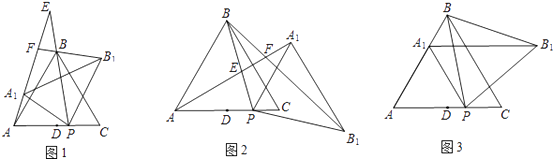
(1)如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在关系(填“相似”或“全等”),并说明理由;
(2)如图2,设∠ABP=β.当60°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图3,当α=60°时,点E、F与点B重合.已知AB=4,设DP=x,△A1BB1的面积为S,求S关于x的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】“魅力数学”社团活动时,张老师出示了如下问题:
如图①,已知四边形ABCD中,AC平分∠DAB,∠DAB=120°,∠B与∠D互补,试探究线段AB,AD,AC之间的数量关系;
小敏反复探索,不得其解,张老师提示道:“数学中常通过把一个问题特殊化来找到解题思路”,于是,小敏想,若将四边形ABCD特殊化,看如何解决问题:
(1)特殊情况入手
添加条件:“∠B=∠D”,如图②易知在Rt△CDA中,∠DCA=30°,所以,写出边AD与AC之间的数量关系,同理可得AB与AC的数量关系,由此得AB,AD,AC之间的数量关系;
(2)解决原来问题
受到(1)的启发,在原问题上,添加辅助线,过点C分别作AB,AD的垂线,垂足分别为E、F,如图③,请写出探究过程;
(3)解后反思
“一题多解”是数学解题的魅力之一,小敏在张老师的引导下,受探究结论的启发,结合图中的60°角,通过构造等边三角形,利用三角形全等同样解决了该问题,请在图①中作出辅助线,并简述你的探究过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价) 甲
乙
进价(元/件)
20
30
售价(元/件)
29
40
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,BC=6,E是BA延长线的一点,P是∠EAC的平分线上一个动点,当△APC是以AC为腰的等腰三角形时,△APC的面积为_____.

相关试题

