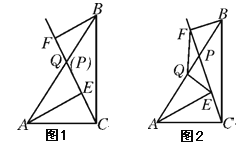
【题目】已知点P是RtABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F。(1)如图1,当点P 为AB 的中点时,连接AF,BE。求证:四边形AEBF是平行四边形;(2)如图2,当点P 不是AB的中点,取AB的中点Q,连接EQ,FQ 。试判断△QEF 的形状,并加以证明。
参考答案:
【答案】(1)证明见解析;(2)△QEF是等腰三角形.证明见解析.
【解析】
试题分析:(1)首先证明△BFQ≌△AEQ可得QE=QF,再由AQ=BQ可利用对角线互相平分的四边形是平行四边形判定四边形AEBF是平行四边形;
(2)首先证明△FBQ≌△DAQ可得QF=QD,再根据直角三角形斜边中线等于斜边的一半可得QE=QF=QD,进而可得结论.
试题解析:(1)如图1,
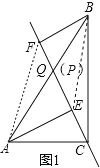
∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,∠BFQ=∠AEQ,
在△BFQ和△AEQ中:
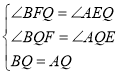
∴△BFQ≌△AEQ(AAS),
∴QE=QF,
∴四边形AEBF是平行四边形;
(2)△QEF是等腰三角形.,
如图2,延长FQ交AE于D,
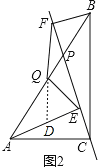
∵AE∥BF,
∴∠QAD=∠FBQ,
在△FBQ和△DAQ中
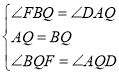 ,
,
∴△FBQ≌△DAQ(ASA),
∴QF=QD,
∵AE⊥CP,
∴EQ是直角三角形DEF斜边上的中线,
∴QE=QF=QD,即QE=QF,
∴△QEF是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大同市在开展的美化城市活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示)。若设花园的BC 长为x(m),花园的面积为y(m2)。
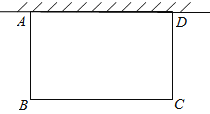
(1)求y与x之间的函数关系式,并写出自变量的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x 的值;若不能,说明理由;(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当x取何值时,花园的面积最大?最大面积为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 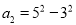 ,……,
,……,  ,(n为正整数)
,(n为正整数)(1)试说明
 是8的倍数;
是8的倍数;(2)若△ABC的三条边长分别为
 、
、 、
、 (
( 为正整数)
为正整数)①求
 的取值范围.
的取值范围.②是否存在这样的
 ,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
 的两个解是
的两个解是 和
和
(1)求
 、
、 的值;
的值;(2)用含有
 的代数式表示
的代数式表示 ;
;(3)若
 是不小于
是不小于 的负数,求
的负数,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a,b,c是△ABC的三条边长,若a=1,b=5,则奇数c=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣1,0,2,3这四个数中,比0小的数是( )
A. ﹣1 B. 0 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆的半径扩大一倍,则它的相应的圆内接正n边形的边长与半径之比( )
A. 扩大了一倍 B. 扩大了两倍 C. 扩大了四倍 D. 没有变化
相关试题

