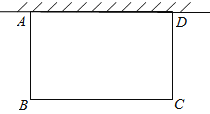
【题目】大同市在开展的美化城市活动中,某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示)。若设花园的BC 长为x(m),花园的面积为y(m2)。
(1)求y与x之间的函数关系式,并写出自变量的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x 的值;若不能,说明理由;(3)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当x取何值时,花园的面积最大?最大面积为多少?
参考答案:
【答案】(1)y=-![]() x2+20x(0<x≤15)(2)花园面积不能达到200m2.理由见解析;(3)当x=15时,花园的面积最大,最大面积为187.5m2.
x2+20x(0<x≤15)(2)花园面积不能达到200m2.理由见解析;(3)当x=15时,花园的面积最大,最大面积为187.5m2.
【解析】
试题分析:(1)设花园靠墙的一边长为x(m),另一边长为![]() ,用面积公式表示矩形面积;
,用面积公式表示矩形面积;
(2)就是已知y=200,解一元二次方程,但要注意检验结果是否符合题意;即结果应该是0<x≤15.
(3)由于0<x≤15,对称轴x=20,即顶点不在范围内,y随x的增大而增大.∴x=15时,y有最大值.
试题解析:(1)根据题意得:y=x×![]() ,
,
即y=-![]() x2+20x(0<x≤15)
x2+20x(0<x≤15)
(2)当y=200时,即-![]() x2+20x=200,
x2+20x=200,
解得x1=x2=20>15,
∴花园面积不能达到200m2.
(3)∵y=-![]() x2+20x的图象是开口向下的抛物线,对称轴为x=20,
x2+20x的图象是开口向下的抛物线,对称轴为x=20,
∴当0<x≤15时,y随x的增大而增大.
∴x=15时,y有最大值,
y最大值=-![]() ×152+20×15=187.5m2
×152+20×15=187.5m2
即当x=15时,花园的面积最大,最大面积为187.5m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式x+2y+1的值是3,则代数式2x+4y+1的值是( )
A. 4 B. 5 C. 7 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】十边形的内角和为( )度.
A. 1800 B. 1260 C. 1440 D. 1620
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC≌△DEF,且△ABC周长为100,AB=35,DF=30,则EF的长为( )
A. 35 B. 30 C. 35 D. 30
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 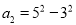 ,……,
,……,  ,(n为正整数)
,(n为正整数)(1)试说明
 是8的倍数;
是8的倍数;(2)若△ABC的三条边长分别为
 、
、 、
、 (
( 为正整数)
为正整数)①求
 的取值范围.
的取值范围.②是否存在这样的
 ,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
 的两个解是
的两个解是 和
和
(1)求
 、
、 的值;
的值;(2)用含有
 的代数式表示
的代数式表示 ;
;(3)若
 是不小于
是不小于 的负数,求
的负数,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
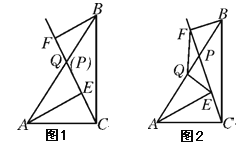
查看答案和解析>>【题目】已知点P是RtABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F。(1)如图1,当点P 为AB 的中点时,连接AF,BE。求证:四边形AEBF是平行四边形;(2)如图2,当点P 不是AB的中点,取AB的中点Q,连接EQ,FQ 。试判断△QEF 的形状,并加以证明。
相关试题

