【题目】如图,△ABC、△ADE中,C、E两点分别在AD、AB上,且BC与DE相交于F点,若∠A=90°,∠B=∠D=30°,AC=AE=1,则四边形AEFC的周长为何( )

A. 2![]() B. 2
B. 2![]() C. 2+
C. 2+![]() D. 2+
D. 2+![]()
参考答案:
【答案】B
【解析】分析:根据三角形的内角和得到∠AED=∠ACB=60°,根据三角形的外角的性质得到∠B=∠EFB=∠CFD=∠D,根据等腰三角形的判定得到BE=EF=CF=CD,于是得到四边形AEFC的周长=AB+AC.
详解:∵∠A=90°,∠B=∠D=30°,
∴∠AED=∠ACB=60°,
∵∠AED=∠B+∠EFB=∠ACB=∠CFD+∠D=60°,
∴∠EFB=∠CFD=30°,
∴∠B=∠EFB=∠CFD=∠D,
∴BE=EF=CF=CD,
∴四边形AEFC的周长=AB+AC,
∵∠A=90°,AE=AC=1,
∴AB=AD=![]() ,
,
∴四边形AEFC的周长=2![]() .
.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA,EC.

(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)如图2,若点P在线段AB的中点,连接AC,判断△ACE的形状,并说明理由;
(3)如图3,若点P在线段AB上,连接AC,当EP平分∠AEC时,设AB=a,BP=b,求a:b及∠AEC的度数.
-
科目: 来源: 题型:
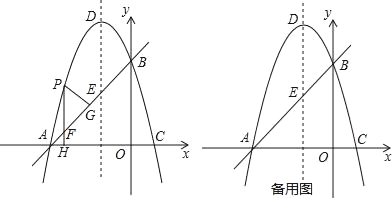
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=﹣x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点,(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线y=﹣x2+bx+c上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在坐标平面内△ABC的顶点坐标分别为A(0,2),B(3,3),C(2,1),(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC关于原点对称的△A1B1C1,并直接写出点C1点的坐标;
(2)画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
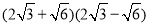 (2)
(2)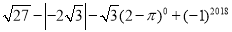
(3)(2
 ﹣
﹣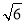 )2+(
)2+(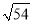 +2
+2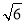 )÷
)÷ .
.(4)
 ﹣(
﹣(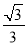 )﹣1+
)﹣1+ (
( ﹣1)﹣20180﹣|
﹣1)﹣20180﹣| ﹣2|.
﹣2|. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班6名同学的身高(单位:cm)情况如下表:
同学
A
B
C
D
E
F
身高
165
166
171
身高与班级平均身高的差值
-1
+2
-3
+3
(1)完成表中空白的部分;
(2)他们的最高身高与最矮身高相差多少?
(3)他们6人的平均身高是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在体育活动课中,体育老师随机抽取了九年级甲、乙两班部分学生进行某体育项目的测试,并对成绩进行统计分析,绘制了频数分布表,请你根据表中的信息完成下列问题:
(1)频数分布表中a= ,b= ;
(2)如果该校九年级共有学生900人,估计该校该体育项目的成绩为良和优的学生有多少人?
(3)已知第一组中有两个甲班学生,第二组中只有一个乙班学生,老师随机从这两个组中各选一名学生对体育活动课提出建议,则所选两人正好是甲班和乙班各一人的概率是多少?
分 组
频数
频率
第一组(不及格)
3
0.15
第二组(中)
b
0.20
第三组(良)
7
0.35
第四组(优)
6
a
相关试题

